题目内容
已知关于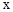 的一元二次方程
的一元二次方程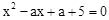 .
.
(1)若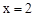 是该方程的一个根,求
是该方程的一个根,求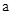 的值;
的值;
(2)无论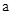 取任何值,该方程的根不可能为
取任何值,该方程的根不可能为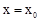 ,写出
,写出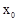 的值,并证明;
的值,并证明;
(3)若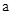 为正整数,且该方程存在正整数解,求所有正整数
为正整数,且该方程存在正整数解,求所有正整数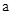 的值.
的值.
【答案】
(1) ;(2)(2)
;(2)(2)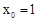 ,证明见解析;(3)
,证明见解析;(3) 或
或 .
.
【解析】
试题分析:(1)根据一元二次方程的根的概念,将 代入方程
代入方程 ,即可求得a的值;(2)把
,即可求得a的值;(2)把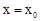 代入
代入 ,得
,得 ,从而得到当
,从而得到当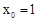 时,无论
时,无论 取何值,此等式均不成立的结论;(3)由
取何值,此等式均不成立的结论;(3)由 ,记
,记 ,
, 为正整数,得
为正整数,得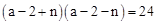 ,根据
,根据 为非负数,且
为非负数,且 ,且
,且 与
与 奇偶性相同的性质,得到
奇偶性相同的性质,得到 或
或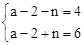 ,解之即得所求.
,解之即得所求.
试题解析:(1)∵ 是方程
是方程 的一个根,∴
的一个根,∴ ,
解得
,
解得 .
.
(2)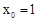 ,证明如下:
,证明如下:
把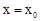 代入
代入 ,得
,得 ,即
,即 ,
,
∴当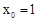 时,无论
时,无论 取何值,此等式均不成立.
取何值,此等式均不成立.
∴无论 取任何值,该方程的根不可能为
取任何值,该方程的根不可能为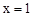 .
.
(3)∵ ,记
,记 ,
, 为正整数,
为正整数,
∴ ,即
,即 ,
,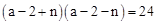 .
.
∵ 为非负数,且
为非负数,且 ,且
,且 与
与 奇偶性相同,
奇偶性相同,
∴ 或
或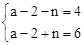 ,解得:
,解得: 或
或 .
.
经验证,当 或
或 时正整数数,符合题意.
时正整数数,符合题意.
考点:1. 一元二次方程的根;2. 一元二次方程根的判别式;3.简单推理.

练习册系列答案
相关题目
 的一元二次方程
的一元二次方程  的一元二次方程
的一元二次方程 的两个整数根恰好比方程
的两个整数根恰好比方程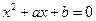 的两个根都大1,求
的两个根都大1,求 的值.
的值.  的一元二次方程x2+2x+m=0.
的一元二次方程x2+2x+m=0. 的一元二次方程
的一元二次方程 有两个不相等的实数根.
有两个不相等的实数根. 的取值范围;
的取值范围;