题目内容
【题目】如图①，△ABC中，AD为BC边上的中线，则有S△ABD＝S△ACD，许多面积问题可以转化为这个基本模型解答．如图②，已知△ABC的面积为1，把△ABC各边均顺次延长一倍，连结所得端点，得到△A1B1C1，即将△ABC向外扩展了一次，则扩展一次后的△A1B1C1的面积是_____，如图③，将△ABC向外扩展了两次得到△A2B2C2，……，若将△ABC向外扩展了n次得到△AnBnn，则扩展n次后得到的△AnBnn面积是_____．
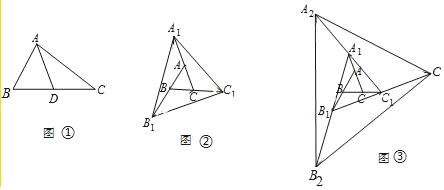
【答案】7， 7n
【解析】
(1)利用三角形的中线将三角形分成面积相等的两个三角形,得出S△ACC
=S△ABC,进而得出S△ACC=2S△ACC=S△ABC,同理:S△AAB=2S△ABC=2,S△BBC=2S△ABC=2,求和即可得出结论
(2)同(1)的方法即可得出结论
(1)∵△ABC各边均顺序延长一倍,
∴BC= CC
∴
=
=1
∴
=2 = =2
同理: S
=2 =2,
=2=2
∴
=+ +
+ =+2
+2
+2=7 =7
（2）由（1）的方法可得
=7=49；
=7=7×7
=343，…以此类推
得出规律
=7
=7
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
