题目内容
如图所示，AB=AD，AD∥BC，∠BDC=90°，∠ABC=∠DCB，则∠ADB等于30
30
度．分析：根据平行线间的内错角可得出∠ADB=∠DBC，根据等腰三角形的性质可得出∠ABD=∠ADB，结合三角形内角和定理可求∠DBC的度数，从而得到∠ADB的度数．
解答：解：∵AB=AD，
∴∠ABD=∠ADB，
∵AD∥BC，
∴∠ADB=∠DBC，
∵∠BDC=90°，∠ABC=∠DCB，
∴∠DBC=（180°-90°）÷3=30°．
∴∠ADB=30°．
故答案为：30．
∴∠ABD=∠ADB，
∵AD∥BC，
∴∠ADB=∠DBC，
∵∠BDC=90°，∠ABC=∠DCB，
∴∠DBC=（180°-90°）÷3=30°．
∴∠ADB=30°．
故答案为：30．
点评：本题重点考查了平行线的性质/等腰三角形的性质和三角形内角和定理，是一道综合题型．
练习册系列答案
相关题目
8、如图所示，AB=AD，∠1=∠2，添加一个适当的条件，使△ABC≌△ADE，则需要添加的条件是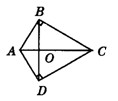
7、如图所示，AB=AD，∠ABC=∠ADC=90°，则①AC平分∠BAD；②CA平分∠BCD；③AC垂直平分BD；④BD平分∠ABC，其中正确的结论有（ ）
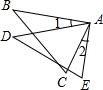（2013•婺城区二模）如图所示，AB=AD，∠1=∠2，添加一个适当的条件，使△ABC≌△ADE（不再添加辅助线，不再标注其他字母）．
如图所示，AB=AD，AC=AE，BC=DE，∠B=28°，∠E=95°，∠EAB=20°，则∠BAD=