题目内容
如图，Q为等边三角形ABC内一点，将△ABQ绕点B旋转，使AB与BC边重合，则∠QBP=________ 度．若BQ=4cm，则△BQP的面积是________．
60 4
cm2
分析：根据旋转的性质证得△ABQ≌CBP，则对应角相等：∠ABQ=∠CBP，BQ=BP，易证△BPQ是正三角形，所以由正三角形的性质来求∠QBP=60°，△BQP的面积．
解答：如图，根据旋转的性质得到：△ABQ≌CBP，则∠ABQ=∠CBP，BQ=BP．
∵△ABC是等边三角形，
∴∠ABQ+∠QBC=∠CBP+∠QBC=60°，即∠QBP=60°，
∴△QBP是等边三角形，
∴S△BQP=
×42×
=4．
故填：60；4cm2．
点评：本题考查了全等三角形的判定与性质，等边三角形的性质．全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．
cm2分析：根据旋转的性质证得△ABQ≌CBP，则对应角相等：∠ABQ=∠CBP，BQ=BP，易证△BPQ是正三角形，所以由正三角形的性质来求∠QBP=60°，△BQP的面积．
解答：如图，根据旋转的性质得到：△ABQ≌CBP，则∠ABQ=∠CBP，BQ=BP．
∵△ABC是等边三角形，
∴∠ABQ+∠QBC=∠CBP+∠QBC=60°，即∠QBP=60°，
∴△QBP是等边三角形，
∴S△BQP=
×42×=4．故填：60；4
cm2．点评：本题考查了全等三角形的判定与性质，等边三角形的性质．全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．
练习册系列答案
天天向上口算本系列答案
相关题目
3、如图，△ABC为等边三角形，∠ABC、∠ACB的平分线相交于点O，OE∥AB交BC于点E，OF∥AC交BC于点F，图中等腰三角形共有（ ）
如图，△ABC为等边三角形，点D，E，F分别在AB，BC，CA边上，且△DEF是等边三角形，求证：△ADF≌△CFE．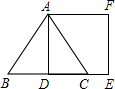
如图，△ABC为等边三角形，AD为BC边上的高，且AB=2，则正方形ADEF的面积为
如图，△ABC为等边三角形，D为△ABC内一点，△ABD逆时针旋转后到达△ACP位置，则∠APD=
如图①，△ABC为等边三角形，周长为p．D1，E1，F1分别是△ABC三边的中点，连接D1E1，E1F1，F1D1，可得△D1E1F1．