题目内容
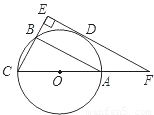
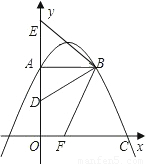
(2010•绍兴)如图为某机械装置的截面图,相切的两圆⊙O1,⊙O2均与⊙O的弧AB相切,且O1O2∥l1(l1为水平线),⊙O1,⊙O2的半径均为30mm,弧AB的最低点到l1的距离为30mm,公切线l2与l1间的距离为100mm.则⊙O的半径为( )
A.70mm
B.80mm
C.85mm
D.100mm
【答案】分析:设⊙O的半径为R,由图可知,CE=100-30=70mm,DE=CE-CD=70-30=40mm,OD=OE-DE=R-40(mm),在Rt△OO1D中,运用勾股定理求R.
解答:解:如图,设⊙O的半径为Rmm,依题意,得
CE=100-30=70(mm),
∵l2∥O1O2,∴CD=O1D=30(mm),
DE=CE-CD=70-30=40(mm),
OD=OE-DE=R-40(mm),
在Rt△OO1D中,O1O=R-30(mm),O1D=30mm,
由勾股定理,得O1D2+OD2=O1O2,
即302+(R-40)2=(R-30)2,
解得R=80mm.故选B.
点评:根据直线与圆相切,圆与圆相切及题中的数量关系,把问题转化到直角三角形中,用勾股定理求解,是解决圆的问题常用的方法.
解答:解:如图,设⊙O的半径为Rmm,依题意,得
CE=100-30=70(mm),
∵l2∥O1O2,∴CD=O1D=30(mm),
DE=CE-CD=70-30=40(mm),
OD=OE-DE=R-40(mm),
在Rt△OO1D中,O1O=R-30(mm),O1D=30mm,
由勾股定理,得O1D2+OD2=O1O2,
即302+(R-40)2=(R-30)2,
解得R=80mm.故选B.
点评:根据直线与圆相切,圆与圆相切及题中的数量关系,把问题转化到直角三角形中,用勾股定理求解,是解决圆的问题常用的方法.

练习册系列答案
相关题目
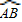 的中点,过点D作直线BC的垂线,分别交CB、CA的延长线E、F.
的中点,过点D作直线BC的垂线,分别交CB、CA的延长线E、F.