Question

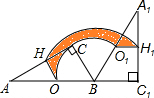如图，Rt△ABC中，∠ACB=90°，∠CAB=30°，BC=2，O、H分别为边AB，AC的中点，将△ABC绕点B顺时针旋转120°到△A₁BC₁的位置，则整个旋转过程中线段OH所扫过部分的面积（即阴影部分面积）为（　　）

• A、

  7

  3

  π-

  7

  8

  3

• B、

  4

  3

  π+

  7

  8

  3

• C、π
• D、

  4

  3

  π+

  3

Answer 1

分析：整个旋转过程中线段OH所扫过部分的面积（即阴影部分面积）为以点B为圆心，OB，BH为半径的两个扇形组成的一个环形．

解答：解：连接BH，BH₁，
∵O、H分别为边AB，AC的中点，将△ABC绕点B顺时针旋转120°到△A₁BC₁的位置，
∴△OBH≌△O₁BH₁，
利用勾股定理可求得BH=

4+3

=

7

，
所以利用扇形面积公式可得

120π(BH2-BC2)

360

=

120π×(7-4)

360

=π．
故选C．

点评：本题的关键是求出半径BH的长，然后利用扇形面积公式就可求．