题目内容
 如图所示,把一张矩形纸片ABCD沿对角线BD折叠,已知AB=6、BC=8,则BF=________.
如图所示,把一张矩形纸片ABCD沿对角线BD折叠,已知AB=6、BC=8,则BF=________.

分析:根据折叠的性质我们可得出AB=ED,∠A=∠E=90°,又有一组对应角,因此就构成了全等三角形判定中的AAS的条件.两三角形就全等,从而设CF为x,解直角三角形ABF可得出答案.
解答:
 解:根据题意可得:AB=DE,∠A=∠E=90°,
解:根据题意可得:AB=DE,∠A=∠E=90°,又∵∠AFB=∠EFD,
∴△ABF≌△EDF(AAS).
∴AF=EF,
设BF=x,则AF=FE=8-x,
在Rt△AFB中,可得:BF2=AB2+AF2,
即x2=62+(8-x)2,
解得:x=
 .
.故答案为:
 .
.点评:本题考查翻折变换的知识,有一定的难度,注意判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目
 19、如图所示,把一张矩形纸片ABCD沿对角线BD折叠,将重合部分剪去,得到△ABF和△EDF.求证:△ABF≌△EDF.
19、如图所示,把一张矩形纸片ABCD沿对角线BD折叠,将重合部分剪去,得到△ABF和△EDF.求证:△ABF≌△EDF.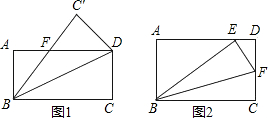 矩形折叠问题:如图所示,把一张矩形纸片沿对角线折叠,重合部分是什么图形,试说明理由.
矩形折叠问题:如图所示,把一张矩形纸片沿对角线折叠,重合部分是什么图形,试说明理由. 如图所示,把一张矩形纸片ABCD沿对角线BD折叠,已知AB=6、BC=8,则BF=
如图所示,把一张矩形纸片ABCD沿对角线BD折叠,已知AB=6、BC=8,则BF=
