题目内容
已知：如图，在∠POQ内部有两点M、N，∠MOP=∠NOQ．
（1）画图并简要说明画法：在射线OP上取一点A，使点A到点M和点N的距离和最小；在射线OQ上取一点B，使点B到点M和点N的距离和最小；
（2）直接写出AM+AN与BM+BN的大小关系．
解：（1）如图所示．
画法：
①作点M关于射线OP的对称点M'，
②连接M'N交OP于点A．
③作点N关于射线OQ的对称点N'，
④连接N'M交OQ于点B．
（2）答：AM+AN与BM+BN的大小关系是：AM+AN=BM+BN．
分析：（1）分别作出点M关于射线OP的对称点M'，点N关于射线OQ的对称点N'，连接M'N、N'M即可求出答案；
（2）关键轴对称性质求出即可．
点评：本题主要考查对轴对称-最短问题的理解和掌握，能正确画图是解此题的关键．
画法：
①作点M关于射线OP的对称点M'，
②连接M'N交OP于点A．
③作点N关于射线OQ的对称点N'，
④连接N'M交OQ于点B．
（2）答：AM+AN与BM+BN的大小关系是：AM+AN=BM+BN．
分析：（1）分别作出点M关于射线OP的对称点M'，点N关于射线OQ的对称点N'，连接M'N、N'M即可求出答案；
（2）关键轴对称性质求出即可．
点评：本题主要考查对轴对称-最短问题的理解和掌握，能正确画图是解此题的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
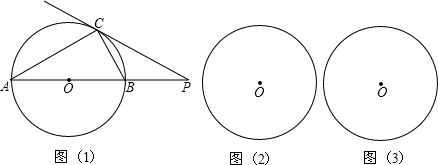
已知：如图AB是半圆0的直径，点C在半圆上，CD⊥AB，垂足为D，切线PC交BA的延长线于点P，AD，DB的长是关于x的方程x2-（4m+2）+4m2=0（m＞0）的两根，且AD：DB=1：4，求：PO、PC的长．
（2004•西藏）已知，如图，P是⊙O外一点，PC切⊙O于点C，割线PO交⊙O于点B、A，且AC=PC．
，且PB=2
