题目内容
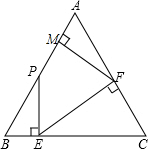 如图.P是等边△ABC边AB上任一点,AB=2,PE⊥BC于E,EF⊥AC于F,FM⊥AB于M,设BP=x(x>0).
如图.P是等边△ABC边AB上任一点,AB=2,PE⊥BC于E,EF⊥AC于F,FM⊥AB于M,设BP=x(x>0).
(1)用含x的代数式表示AM;
(2)当x等于多少时,点P和点M重合?
解:(1)∵△ABC是等边三角形,
∴AB=BC=AC=2,∠B=∠C=∠A=60°,
∵PE⊥BC,EF⊥AC,FM⊥AB,
∴∠PEB=∠EFC=∠FMA=90°,
∴由三角形内角和定理得:∠BPE=∠FEC=∠AFM=30°,
∵BE= BP,CF=
BP,CF= CE,AM=
CE,AM= AF,
AF,
∵BP=x,AB=BC=AC=2,
∴BE= x,CE=2-
x,CE=2- x,CF=
x,CF= CE=1-
CE=1- x,AF=2-CF=2-(1-
x,AF=2-CF=2-(1- x)=1+
x)=1+ x,
x,
∴AM= AF=
AF= +
+ x.
x.
(2)当P和M重合时,AM+PB=AB=2,
即x+ +
+ x=2,
x=2,
x= ,
,
即当x= 时,点P和点M重合.
时,点P和点M重合.
分析:(1)根据等边三角形的性质得出AB=BC=AC=2,∠B=∠C=∠A=60°,根据三角形内角和定理求出∠BPE=∠FEC=∠AFM=30°,推出BE= BP,CF=
BP,CF= CE,AM=
CE,AM= AF,代入求出即可;
AF,代入求出即可;
(2)当P和M重合时得出方程x+ +
+ x=2,求出方程的解即可.
x=2,求出方程的解即可.
点评:本题考查了三角形的内角和定理,含30度角的直角三角形性质,等边三角形的性质的应用,关键是用x把各个线段表示出来.
∴AB=BC=AC=2,∠B=∠C=∠A=60°,
∵PE⊥BC,EF⊥AC,FM⊥AB,
∴∠PEB=∠EFC=∠FMA=90°,
∴由三角形内角和定理得:∠BPE=∠FEC=∠AFM=30°,
∵BE=
 BP,CF=
BP,CF= CE,AM=
CE,AM= AF,
AF,∵BP=x,AB=BC=AC=2,
∴BE=
 x,CE=2-
x,CE=2- x,CF=
x,CF= CE=1-
CE=1- x,AF=2-CF=2-(1-
x,AF=2-CF=2-(1- x)=1+
x)=1+ x,
x,∴AM=
 AF=
AF= +
+ x.
x.(2)当P和M重合时,AM+PB=AB=2,
即x+
 +
+ x=2,
x=2,x=
 ,
,即当x=
 时,点P和点M重合.
时,点P和点M重合.分析:(1)根据等边三角形的性质得出AB=BC=AC=2,∠B=∠C=∠A=60°,根据三角形内角和定理求出∠BPE=∠FEC=∠AFM=30°,推出BE=
 BP,CF=
BP,CF= CE,AM=
CE,AM= AF,代入求出即可;
AF,代入求出即可;(2)当P和M重合时得出方程x+
 +
+ x=2,求出方程的解即可.
x=2,求出方程的解即可.点评:本题考查了三角形的内角和定理,含30度角的直角三角形性质,等边三角形的性质的应用,关键是用x把各个线段表示出来.

练习册系列答案
相关题目
 如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于
如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于 如图,△ABC是等边三角形,点D是线段BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,连接BE.
如图,△ABC是等边三角形,点D是线段BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,连接BE. 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.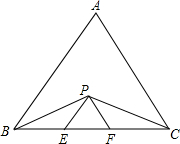 如图,△ABC是等边三角形,P为△ABC内任意一点,PE∥AB,PF∥AC.那么,△PEF是什么三角形?说明理由.
如图,△ABC是等边三角形,P为△ABC内任意一点,PE∥AB,PF∥AC.那么,△PEF是什么三角形?说明理由.