Question

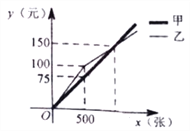
【题目】某社区准备进行“为了地球，远离白色污染”的宣传活动，需要制定宣传单，选择社区附近的甲、乙两家印刷社印刷，他们各自制作这种宣传单的费用y（元）与宣传单数量x（张）之间的函数图象如图所示，结合图象解答下列问题：

（1）求甲印刷社制作这种宣传单每张的钱数.

（2）当x>500时，求乙印刷社所需的费用y与x之间的函数关系式.

（3）如果该社区在制作这种宣传单时，第一次印刷了800张宣传单，第二次印刷了1200张宣传单，直接写出该社区两次印刷这种宣传单共花费的最少钱数.

Answer 1

【答案】（1）甲印刷社制作此种宣传单每张0.15元；（2）；（3）该社区印制两次这种宣传单共花费最少为290元．

【解析】试题分析：（1）根据图象可得结论；

（2）根据甲图象求出当y=150时所印制张数，然后根据待定系数法求出乙印刷社所需的费用y与x之间的函数关系式；

（3）前800张在甲印刷社制作，后1200张在乙印刷社制作，把两者的花费相加即可．

试题解析：解：（1）75÷500=0.15（元）．

答：甲印刷社制作此种宣传单每张0.15元．

（2）当时，设乙印刷社所需的费用与之间的函数关系式为．

∵，∴直线经过点．

由题意得：

解得：

∴．

（3）前800张在甲印刷社制作，花费：800×0.15=120（元），后1200张在乙印刷社制作，花费：0.1×1200+50=170（元），一共花费：120+170=290（元）．

答：该社区印制两次这种宣传单共花费最少为290元．