题目内容
 如图,⊙O的半径为3cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以πcm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为( )s时,BP与⊙O相切.
如图,⊙O的半径为3cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以πcm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为( )s时,BP与⊙O相切.分析:根据切线的判定与性质进行分析即可.若BP与⊙O相切,则∠OPB=90°,又因为OB=2OP,可得∠B=30°,则∠BOP=60°;根据弧长公式求得弧AP长,除以速度,即可求得时间.
解答:解:连接OP;
∵当OP⊥PB时,BP与⊙O相切,
∵AB=OA,OA=OP,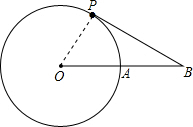
∴OB=2OP,∠OPB=90°;
∴∠B=30°;
∴∠O=60°;
∵OA=3cm,
弧AP=
=π,
∵圆的周长为:6π,
∴点P运动的距离为π或6π-π=5π;
∴当t=1或5时,有BP与⊙O相切.
故选C.
∵当OP⊥PB时,BP与⊙O相切,
∵AB=OA,OA=OP,

∴OB=2OP,∠OPB=90°;
∴∠B=30°;
∴∠O=60°;
∵OA=3cm,
弧AP=
| 60•π•3 |
| 180 |
∵圆的周长为:6π,
∴点P运动的距离为π或6π-π=5π;
∴当t=1或5时,有BP与⊙O相切.
故选C.
点评:本题考查的是切线的性质及弧长公式,解答此题时要注意过圆外一点有两条直线与圆相切,不要漏解.

练习册系列答案
相关题目
 如图,⊙O的半径为5,AB=5
如图,⊙O的半径为5,AB=5 如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2=
如图,⊙O的半径为3,直径AB⊥弦CD,垂足为E,点F是BC的中点,那么EF2+OF2= 如图,⊙O的半径为
如图,⊙O的半径为 如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离.
如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离. 如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为
如图,⊙O的半径为5,P是弦MN上的一点,且MP:PN=1:2.若PA=2,则MN的长为