题目内容
 如图,将边长为8的等边△AOB置于平面直角坐标系中,点A在x轴正半轴上,过点O作OC⊥AB于点C,将△OAC绕着原点O逆时针旋转60°得到△OBD,这时,点D恰好落在y轴上.若动点E从原点O出发,沿线段OC向终点C运动,动点F从点D出发,沿线段DO向终点O运动,两点同时出发,速度均为每秒1个单位长度.设运动的时间为t秒.
如图,将边长为8的等边△AOB置于平面直角坐标系中,点A在x轴正半轴上,过点O作OC⊥AB于点C,将△OAC绕着原点O逆时针旋转60°得到△OBD,这时,点D恰好落在y轴上.若动点E从原点O出发,沿线段OC向终点C运动,动点F从点D出发,沿线段DO向终点O运动,两点同时出发,速度均为每秒1个单位长度.设运动的时间为t秒.(1)请直接写出点A、点D的坐标;
(2)当△OEF的面积为
3
| ||
| 4 |
(3)设EF与OB相交于点P,当t为何值时,△OPF与△OBD相似?
分析:(1)根据等边三角形的性质可直接得出A点坐标;再由OC⊥AB可得出OC的长,根据图形旋转不变性的性质可得出OD的长,进而得出D点坐标;
(2)过点E作EG⊥OD于点G,根据等边三角形的性质可知OC平分∠AOB,再根据锐角三角函数的定义求出EG的长,S△OEF=
OF•EG,OF=OD-DF=4
-t即可得出t的值;
(3)由于∠BOD=∠FOP,△OPF∽△ODB和△OPF∽△OBD两种情况进行讨论.
(2)过点E作EG⊥OD于点G,根据等边三角形的性质可知OC平分∠AOB,再根据锐角三角函数的定义求出EG的长,S△OEF=
| 1 |
| 2 |
| 3 |
(3)由于∠BOD=∠FOP,△OPF∽△ODB和△OPF∽△OBD两种情况进行讨论.
解答: 解:(1)∵等边△AOB的边长为8,点A在x轴正半轴上,
解:(1)∵等边△AOB的边长为8,点A在x轴正半轴上,
∴A(8,0),
∵OC⊥AB,
∴∠AOC=30°,
∴OC=OA•cos30°=8×
=4
,
∵△OAC旋转后OC与OD重合,
∴D(0,4
);
(2)过点E作EG⊥OD于点G,如图①所示:
∵△OAB为等边三角形,OC⊥AB,
∴OC平分∠AOB,
∴∠AOC=30°,
∴∠EOG=90°-30°=60°,
∴EG=OE•sin∠EOG=
t,
又∵S△OEF=
OF•EG,OF=OD-DF=4
-t,
由题意可得:
(4
-t)•
t=
解得t=2
±3;
(3)因为∠BOD=∠FOP,所以应分两种情况讨论:
①当∠FPO=∠BDO=90°时,如图②,
∵△OPF∽△ODB,此时OE=OF,
∴t=4
-t,解得:t=2
;
②当∠OFP=∠ODB=90°时,如图③,
∵△OPF∽△OBD,
∴OF=
OE,即(4
-t)=
t,
解得:t=
.
综上所述,当t=2
秒或t=
秒时,△OPF与△OBD相似.
 解:(1)∵等边△AOB的边长为8,点A在x轴正半轴上,
解:(1)∵等边△AOB的边长为8,点A在x轴正半轴上,∴A(8,0),
∵OC⊥AB,
∴∠AOC=30°,
∴OC=OA•cos30°=8×
| ||
| 2 |
| 3 |
∵△OAC旋转后OC与OD重合,
∴D(0,4
| 3 |
(2)过点E作EG⊥OD于点G,如图①所示:
∵△OAB为等边三角形,OC⊥AB,
∴OC平分∠AOB,
∴∠AOC=30°,
∴∠EOG=90°-30°=60°,
∴EG=OE•sin∠EOG=
| ||
| 2 |
又∵S△OEF=
| 1 |
| 2 |
| 3 |
由题意可得:
| 1 |
| 2 |
| 3 |
| ||
| 2 |
3
| ||
| 4 |
解得t=2
| 3 |
(3)因为∠BOD=∠FOP,所以应分两种情况讨论:
①当∠FPO=∠BDO=90°时,如图②,
∵△OPF∽△ODB,此时OE=OF,
∴t=4
| 3 |
| 3 |
②当∠OFP=∠ODB=90°时,如图③,
∵△OPF∽△OBD,
∴OF=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
解得:t=
8
| ||
| 3 |
综上所述,当t=2
| 3 |
8
| ||
| 3 |
点评:本题考查的是相似形综合题,涉及到相似三角形的判定与性质、等边三角形的性质等知识,在解答(3)时要注意进行分类讨论,不要漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
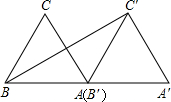 如图,将边长为3的等边△ABC沿着
如图,将边长为3的等边△ABC沿着| BA |
A、
| ||
B、2
| ||
C、3
| ||
D、4
|
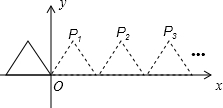 如图,将边长为2的等边三角形沿x轴正方向连续翻折2012次,依次得到点P1,P2,P3…P2012.则点P2012的坐标是
如图,将边长为2的等边三角形沿x轴正方向连续翻折2012次,依次得到点P1,P2,P3…P2012.则点P2012的坐标是 (2013•遵义)如图,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为( )
(2013•遵义)如图,将边长为1cm的等边三角形ABC沿直线l向右翻动(不滑动),点B从开始到结束,所经过路径的长度为( )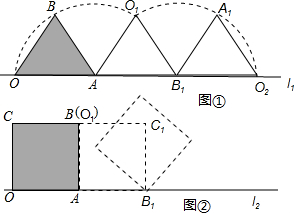
 如图,将边长为6cm的等边三角形△ABC沿BC方向向右平移后得△DEF,DE、AC相交于点G,若线段CF=4cm,则△GEC的周长是
如图,将边长为6cm的等边三角形△ABC沿BC方向向右平移后得△DEF,DE、AC相交于点G,若线段CF=4cm,则△GEC的周长是