题目内容
 如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,直线BE交AC于点F,若△ABC的面积为24,则△AEF的面积为
如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,直线BE交AC于点F,若△ABC的面积为24,则△AEF的面积为考点:三角形的面积
专题:
分析:先过D作DG∥BF,交AC于G,设S△AEF=x,S△CDG=y,由于△ABC的面积为24,BD=CD,可求S△ABD,S△ACD,又因为E是AD中点,可求S△ABE.在△ADG中,DG∥BF,E是AD中点,利用平行线分线段成比例定理的推论,可知AF=FG,从而可知△AEF∽△ADG,再利用相似三角形的面积比等于相似比的平方,可得∴S△ADG=4x,同理可求S△BCF=4y,再利用三角形面积之间的加减关系可得关于x、y的二元一次方程,求解即可.
解答: 解:过D作DG∥BF,交AC于G,设S△AEF=x,S△CDG=y,
解:过D作DG∥BF,交AC于G,设S△AEF=x,S△CDG=y,
∵△ABC的面积为24,BD=CD,
∴S△ABD=S△ACD=
×S△ABC=12,
又∵E是AD中点,
∴S△ABE=S△BDE=
×S△ABD=6,
在△ADG中,∵DG∥BF,E是AD中点,
∴S△AEF:S△ADG=1:4,
∴S△ADG=4x,
同理在△BCF中,∵DG∥BF,BD=CD,
∴S△BCF=4y,
则有
,
解得
,
则△AEF的面积为2.
故答案为:2.
 解:过D作DG∥BF,交AC于G,设S△AEF=x,S△CDG=y,
解:过D作DG∥BF,交AC于G,设S△AEF=x,S△CDG=y,∵△ABC的面积为24,BD=CD,
∴S△ABD=S△ACD=
| 1 |
| 2 |
又∵E是AD中点,
∴S△ABE=S△BDE=
| 1 |
| 2 |
在△ADG中,∵DG∥BF,E是AD中点,
∴S△AEF:S△ADG=1:4,
∴S△ADG=4x,
同理在△BCF中,∵DG∥BF,BD=CD,
∴S△BCF=4y,
则有
|
解得
|
则△AEF的面积为2.
故答案为:2.
点评:本题考查了三角形的面积计算、平行线分线段成比例的推论、相似三角形的判定、相似三角形的面积比等于相似比的平方.关键是作辅助线,所作的平行线能用到两个三角形中.

练习册系列答案
相关题目
下列计算中正确的是( )
| A、y6÷y6=1 |
| B、(3ab2)2=6a2b4 |
| C、a3•a2=a6 |
| D、y6+y6=2y12 |
下列计算中正确的是( )
| A、2x+3y=5xy |
| B、x•x4=x4 |
| C、x8÷x2=x6 |
| D、(x-y)2=x2-y2 |
 如图,l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为
如图,l∥m,等腰直角三角形ABC的直角顶点C在直线m上,若∠β=20°,则∠α的度数为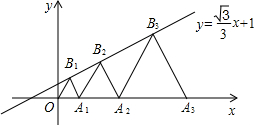 如图,点A1、A2、A3、…在平面直角坐标系x轴上,点B1、B2、B3、…在直线y=
如图,点A1、A2、A3、…在平面直角坐标系x轴上,点B1、B2、B3、…在直线y= 如图,两建筑物的水平距离BC=24米,从点A测得点D的俯角α=30°,点C的俯角β=45°则建筑物CD的高度为
如图,两建筑物的水平距离BC=24米,从点A测得点D的俯角α=30°,点C的俯角β=45°则建筑物CD的高度为