题目内容
 如图,在△AMN中,AM=AN,点B,C分别在MN所在的直线上,且BM=CN.试判断△ABC的形状,并说明理由.
如图,在△AMN中,AM=AN,点B,C分别在MN所在的直线上,且BM=CN.试判断△ABC的形状,并说明理由.
解:△ABC是等腰三角形.理由:
∵AM=AN
∴∠M=∠N
∵BM=CN
∴△AMB≌△ANC
∴AB=AC
∴△ABC是等腰三角形.
分析:由题中所给条件可知AM=AN,可知∠M=∠N,又BM=CN,从而得到两个三角形全等,根据全等三角形的性质,可知AB=AC,从而得到△ABC是等腰三角形.
点评:本题考查了等腰三角形的判定及全等三角形的判定与性质;解本题要充分利用条件,先证明△AMB≌△ANC得出AB=AC是正确解答本题的关键.
∵AM=AN
∴∠M=∠N
∵BM=CN
∴△AMB≌△ANC
∴AB=AC
∴△ABC是等腰三角形.
分析:由题中所给条件可知AM=AN,可知∠M=∠N,又BM=CN,从而得到两个三角形全等,根据全等三角形的性质,可知AB=AC,从而得到△ABC是等腰三角形.
点评:本题考查了等腰三角形的判定及全等三角形的判定与性质;解本题要充分利用条件,先证明△AMB≌△ANC得出AB=AC是正确解答本题的关键.

练习册系列答案
相关题目
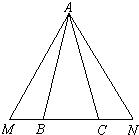 22、如图,在△AMN中,AM=AN,点B,C分别在MN所在的直线上,且BM=CN.试判断△ABC的形状,并说明理由.
22、如图,在△AMN中,AM=AN,点B,C分别在MN所在的直线上,且BM=CN.试判断△ABC的形状,并说明理由.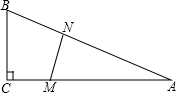 (2013•莲湖区一模)如图,在△ABC中,∠C=90°,BC=5米,AC=12米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.△AMN的最大面积是
(2013•莲湖区一模)如图,在△ABC中,∠C=90°,BC=5米,AC=12米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.△AMN的最大面积是 已知:如图,在⊙O中M,N分别为弦AB,CD的中点,AB=CD,AB不平行于CD.
已知:如图,在⊙O中M,N分别为弦AB,CD的中点,AB=CD,AB不平行于CD. 如图,在△ABC中,OB、OC分别是∠B和∠C的平分线,过O作MN∥BC.若AB=12,AC=18,BC=24,则△AMN的周长.
如图,在△ABC中,OB、OC分别是∠B和∠C的平分线,过O作MN∥BC.若AB=12,AC=18,BC=24,则△AMN的周长.