题目内容
三角形的三条边各不相同,并且其三条高都是整数,其中有两条分别是3和10,那么第三条高的长度为________.
4
分析:设面积的2倍为1,有两条分别是3和10,则a= ,b=
,b= ,根据三角形的任意两边之和一定要大于第三边,求出c边的范围,再进一步求出c边上高的范围即可得出答案.
,根据三角形的任意两边之和一定要大于第三边,求出c边的范围,再进一步求出c边上高的范围即可得出答案.
解答:设面积的2倍为1,
∵两条分别是3和10,
则a= ,b=
,b= ,根据三角形的任意两边之和一定要大于第三边,所以c边的长度在
,根据三角形的任意两边之和一定要大于第三边,所以c边的长度在 +
+ =
= 和
和 -
- =
=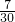 之间,
之间,
∴c边上的高的长度则在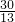 到
到 之间,
之间,
即大于2.2,小于4.5 整数只有3和4两个,
又因为三边各不相等,高也不可能相等,所以只能是4.
故答案为:4.
点评:本题考查了三角形三边关系,难度较大,关键是设面积的2倍为1,根据三角形的任意两边之和一定要大于第三边求出c边的范围.
分析:设面积的2倍为1,有两条分别是3和10,则a=
 ,b=
,b= ,根据三角形的任意两边之和一定要大于第三边,求出c边的范围,再进一步求出c边上高的范围即可得出答案.
,根据三角形的任意两边之和一定要大于第三边,求出c边的范围,再进一步求出c边上高的范围即可得出答案.解答:设面积的2倍为1,
∵两条分别是3和10,
则a=
 ,b=
,b= ,根据三角形的任意两边之和一定要大于第三边,所以c边的长度在
,根据三角形的任意两边之和一定要大于第三边,所以c边的长度在 +
+ =
= 和
和 -
- =
=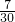 之间,
之间,∴c边上的高的长度则在
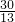 到
到 之间,
之间,即大于2.2,小于4.5 整数只有3和4两个,
又因为三边各不相等,高也不可能相等,所以只能是4.
故答案为:4.
点评:本题考查了三角形三边关系,难度较大,关键是设面积的2倍为1,根据三角形的任意两边之和一定要大于第三边求出c边的范围.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目