题目内容
如图，AB为⊙O的切线，B为切点．若∠A=30°，AO=6，则OB= ．
【答案】分析：由切线性质知△OAB为直角三角形，从而在Rt△OAB中通过解直角三角形求得OB的长．
解答：解：∵AB为⊙O的切线，B为切点，
∴∠OBA=90°；
在Rt△OAB中，∠A=30°，OA=6；
∴OB=AO•sinA=3．
点评：本题考查了圆的切线性质，及解直角三角形的知识．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
解答：解：∵AB为⊙O的切线，B为切点，
∴∠OBA=90°；
在Rt△OAB中，∠A=30°，OA=6；
∴OB=AO•sinA=3．
点评：本题考查了圆的切线性质，及解直角三角形的知识．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
练习册系列答案
相关题目
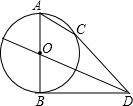已知：如图，AB为⊙O的直径，弦AC∥OD，BD切⊙O于B，连接CD．
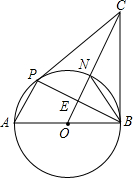如图，AB为⊙O的直径，BC⊥AB，CP切⊙O于点P，连OC，交⊙O于N，交BP于E，连BN，AP．
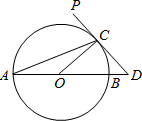（2012•洛阳二模）如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于D，且CO=CD，则∠PCA=
已知：如图，AB为⊙O的弦，P为AB延长线上的一点，PC切⊙O于C，CD为⊙O的直径，CD交AB于E，DE=2，AE=3，BE=6，则PB=（ ）
如图，AB为⊙O的直径，EF切⊙O于点D，过点B作BH⊥EF于点H，交⊙O于点C，连接BD．若∠ABH=50°，则∠ABD的度数是（ ）