ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЖўДЮКЏЪ§![]() ЕФЭМЯёгы
ЕФЭМЯёгы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгк
жсНЛгк![]() ЕуЃЌЕу
ЕуЃЌЕу![]() ЪЧХзЮяЯпЖЅЕуЃЌЕу
ЪЧХзЮяЯпЖЅЕуЃЌЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЯТЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЎ
ЯТЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЎ
ЃЈ![]() ЃЉетИіЖўДЮКЏЪ§ЕФБэДяЪНЮЊ____________ЃЎ
ЃЉетИіЖўДЮКЏЪ§ЕФБэДяЪНЮЊ____________ЃЎ
ЃЈ![]() ЃЉЩшжБЯп
ЃЉЩшжБЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌдђВЛЕШЪН
ЃЌдђВЛЕШЪН![]() ЕФНтМЏЮЊ___________ЃЎ
ЕФНтМЏЮЊ___________ЃЎ
ЃЈ![]() ЃЉСЌНс
ЃЉСЌНс![]() ЁЂ
ЁЂ![]() ЃЌВЂАб
ЃЌВЂАб![]() би
би![]() ЗелЃЌЕУЕНЫФБпаЮ
ЗелЃЌЕУЕНЫФБпаЮ![]() ЃЌФЧУДЪЧЗёДцдкЕу
ЃЌФЧУДЪЧЗёДцдкЕу![]() ЃЌЪЙЫФБпаЮ
ЃЌЪЙЫФБпаЮ![]() ЮЊСтаЮЃПШєДцдкЃЌЧыЧѓГіДЫЪБЕу
ЮЊСтаЮЃПШєДцдкЃЌЧыЧѓГіДЫЪБЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ![]() ЃЉЕБЫФБпаЮ
ЃЉЕБЫФБпаЮ![]() ЕФУцЛ§зюДѓЪБЃЌЧѓГіДЫЪБ
ЕФУцЛ§зюДѓЪБЃЌЧѓГіДЫЪБ![]() ЕуЕФзјБъКЭЫФБпаЮ
ЕуЕФзјБъКЭЫФБпаЮ![]() ЕФзюДѓУцЛ§ЃЎ
ЕФзюДѓУцЛ§ЃЎ
ЃЈ![]() ЃЉШєАбЬѕМўЁАЕу
ЃЉШєАбЬѕМўЁАЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЯТЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЎЁБИФЮЊЁАЕу
ЯТЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЎЁБИФЮЊЁАЕу![]() ЪЧХзЮяЯпЩЯЕФШЮвЛЖЏЕуЁБЃЌЦфЫќЬѕМўВЛБфЃЌЕБвд
ЪЧХзЮяЯпЩЯЕФШЮвЛЖЏЕуЁБЃЌЦфЫќЬѕМўВЛБфЃЌЕБвд![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮЊЖЅЕуЕФЫФБпаЮЮЊЬнаЮЪБЃЌжБНгаДГіЕу
ЮЊЖЅЕуЕФЫФБпаЮЮЊЬнаЮЪБЃЌжБНгаДГіЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
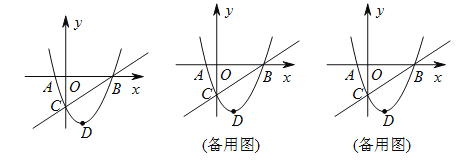
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉxЁм0ЛђxЁн3ЃЛЃЈ3ЃЉ
ЃЛЃЈ2ЃЉxЁм0ЛђxЁн3ЃЛЃЈ3ЃЉ![]() ЃЛЃЈ4ЃЉЕБPЃЈ
ЃЛЃЈ4ЃЉЕБPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЪБЃЌSЫФБпаЮABPCзюДѓ
ЃЉЪБЃЌSЫФБпаЮABPCзюДѓ![]() ЃЛЃЈ5ЃЉЕуPЕФзјБъЮЊЃЈЃ2ЃЌ5ЃЉЃЌЃЈ2ЃЌЃ3ЃЉЛђЃЈ4ЃЌ5ЃЉЃЎ
ЃЛЃЈ5ЃЉЕуPЕФзјБъЮЊЃЈЃ2ЃЌ5ЃЉЃЌЃЈ2ЃЌЃ3ЃЉЛђЃЈ4ЃЌ5ЃЉЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉжБНгЩшГЩЖЅЕуЪНМДПЩЕУГіХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉЯШШЗЖЈГіЕуBЃЌCзјБъЃЌдйИљОнЭМЯѓжБНгаДГіЗЖЮЇЃЛ
ЃЈ3ЃЉРћгУСтаЮЕФаджЪЕУГіPO=PCМДПЩЕУГіЕуPЕФзнзјБъЃЌДњШыХзЮяЯпНтЮіЪНМДПЩЕУГіНсТлЃЛ
ЃЈ4ЃЉЯШРћгУзјБъЯЕжаМИКЮЭМаЮЕФУцЛ§ЕФМЦЫуЗНЗЈНЈСЂКЏЪ§ЙиЯЕЪНМДПЩЧѓГіУцЛ§ЕФзюДѓжЕЃЛ
ЃЈ5ЃЉЯШЧѓГіжБЯпBCЃЌBCЃЌCDЕФНтЮіЪНЃЌЗжШ§жжЧщПіРћгУЬнаЮЕФаджЪЃЌвЛзщЖдБпЦНааМДПЩЕУГіжБЯпDP1ЃЌCP2ЃЌBP3ЕФНтЮіЪНЃЌЗжБ№СЊСЂХзЮяЯпЕФНтЮіЪННЈСЂЗНГЬзщЧѓНтМДПЩЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉЁпЕуDЃЈ1ЃЌЉ4ЃЉЪЧХзЮяЯпy=x2+bx+cЕФЖЅЕуЃЌЁрy=ЃЈxЉ1ЃЉ2Љ4=x2Љ2xЉ3ЃЎЙЪД№АИЮЊЃКy=x2Љ2xЉ3ЃЛ
ЃЈ2ЃЉСюx=0ЃЌЁрy=Љ3ЃЌЁрCЃЈ0ЃЌЉ3ЃЉЃЌСюy=0ЃЌЁрx2Љ2xЉ3=0ЃЌЁрx=Љ1Лђx=3ЃЌЁрAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌЁрВЛЕШЪНx2+bx+cЁнkx+mЕФНтМЏЮЊxЃМ0ЛђЃО3ЃЎЙЪД№АИЮЊЃКxЃМ0ЛђЃО3ЃЛ
ЃЈ3ЃЉШчЭМ1ЃЎЁпЫФБпаЮPOPЁфCЮЊСтаЮЃЌЁрPO=PCЃЎЁпCЃЈ0ЃЌЉ3ЃЉЃЌЁрЕуPЕФзнзјБъЮЊЉ![]() ЃЎЁпPдкХзЮяЯпy=x2Љ2xЉ3ЩЯЃЌЁрЉ
ЃЎЁпPдкХзЮяЯпy=x2Љ2xЉ3ЩЯЃЌЁрЉ![]() =x2Љ2xЉ3ЃЌЁрx=
=x2Љ2xЉ3ЃЌЁрx=![]() Лђx=
Лђx=![]() ЃЈЩсЃЉЃЌЁрPЃЈ
ЃЈЩсЃЉЃЌЁрPЃЈ![]() ЃЎЉ
ЃЎЉ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ4ЃЉШчЭМ2ЃЌгЩЃЈ1ЃЉжЊЃЌBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ3ЃЉЃЌЁржБЯпBCЕФНтЮіЪНЮЊy=xЉ3ЃЌЙ§ЕуPзїPEЁЮyжсНЛBCгкEЃЌЩшPЃЈmЃЌm2Љ2mЉ3ЃЉЃЌЃЈ0ЃМmЃМ3ЃЉ
ЁрEЃЈmЃЌmЉ3ЃЉЃЌЁрPE=mЉ3ЉЃЈm2Љ2mЉ3ЃЉ=Љm2+3mЃЎЁпAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ3ЃЉЃЌЁрSЫФБпаЮABPC=SЁїABC+SЁїPCE+SЁїPBE=![]() ABOC+
ABOC+![]() PE|xP|+
PE|xP|+![]() PE|xBЉxP|
PE|xBЉxP|
=![]() ABOC+
ABOC+![]() PEЃЈ|xP|+|xBЉxP|ЃЉ=
PEЃЈ|xP|+|xBЉxP|ЃЉ=![]() ЁС4ЁС3+
ЁС4ЁС3+![]() ЃЈЉm2+3mЃЉЁСЃЈm+3ЉmЃЉ
ЃЈЉm2+3mЃЉЁСЃЈm+3ЉmЃЉ
=6+![]() ЁСЃЈЉm2+3mЃЉ=Љ
ЁСЃЈЉm2+3mЃЉ=Љ![]() ЃЈmЉ
ЃЈmЉ![]() ЃЉ2+
ЃЉ2+![]()
ЕБm=![]() ЪБЃЌSЫФБпаЮABPCзюДѓ=
ЪБЃЌSЫФБпаЮABPCзюДѓ=![]() ЃЎ
ЃЎ
ЕБm=![]() ЪБЃЌm2Љ2mЉ3=
ЪБЃЌm2Љ2mЉ3=![]() ЃЌЁрPЃЈ
ЃЌЁрPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ5ЃЉШчЭМЃЌгЩЃЈ1ЃЉжЊЃЌBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ3ЃЉЃЌDЃЈ1ЃЌЉ4ЃЉЃЌЁржБЯпBCЕФНтЮіЪНЮЊy=xЉ3ЃЌжБЯпBDЕФНтЮіЪНЮЊy=2xЉ6ЃЌжБЯпCDЕФНтЮіЪНЮЊy=ЉxЉ3ЃЎЁпвдPЁЂCЁЂDЁЂBЮЊЖЅЕуЕФЫФБпаЮЮЊЬнаЮЃЎЁпХзЮяЯпЕФНтЮіЪНЮЊy=x2Љ2xЉ3ЂйЃЛ
ЂйЕБDP1ЁЮBCЪБЃЌЁржБЯпDP1ЕФНтЮіЪНЮЊy=xЉ5ЂкЃЌСЊСЂЂйЂкНтЕУЃЌЕуP1ЃЈ2ЃЌЉ3ЃЉЃЌ[СэвЛИіЕуЮЊЃЈ1ЃЌЉ4ЃЉКЭЕуDжиКЯЃЌЩсШЅ]
ЂкЕБCP2ЁЮBDЪБЃЌЁржБЯпCP2ЕФНтЮіЪНЮЊy=2xЉ3ЂлЃЌСЊСЂЂйЂлНтЕУЕуP2ЃЈ4ЃЌ5ЃЉ
ЂлЕБBP3ЁЮCDЪБЃЌЁржБЯпBP3ЁЮCDЕФНтЮіЪНЮЊy=Љx+3ЂмЃЌСЊСЂЂйЂмНтЕУЕуP3ЃЈЉ2ЃЌ5ЃЉЃЎ
злЩЯЫљЪіЃКвдPЁЂCЁЂDЁЂBЮЊЖЅЕуЕФЫФБпаЮЮЊЬнаЮЪБЃЌЕуPЕФзјБъЮЊЃЈЉ2ЃЌ5ЃЉЁЂЃЈ2ЃЌЉ3ЃЉЛђЃЈ4ЃЌ5ЃЉЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ