题目内容
6. 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A顺时针方向旋转90°得到△AB′C′
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A顺时针方向旋转90°得到△AB′C′(1)在正方形网格中,画出△AB′C′;
(2)求出四边形BCB′C′的面积;
(3)设点P(a,b)是△ABC边上的一点,点P绕点A顺时针方向旋转90°后的对应点是P′,则点P′的坐标为(b,-a).
分析 (1)根据图形旋转的性质画出△A′B′C′即可;
(2)利用S四边形BCB′C′=S△BC′E-S△B′CE即可得出结论;
(3)先求出点B与点B′的坐标,找出规律即可得出结论.
解答  解:(1)如图,△A′B′C′即为所求;
解:(1)如图,△A′B′C′即为所求;
(2)S四边形BCB′C′=S△BC′E-S△B′CE=$\frac{1}{2}$×4×7-$\frac{1}{2}$×1×4=14-2
=12;
(3)∵B(4,3),B′(3,-4),P(a,b),
∴P(b,-a).
故答案为:(b,-a).
点评 本题考查的是作图-旋转变换,熟知图形旋转的性质是解答此题的关键.

练习册系列答案
相关题目
16.16的算术平方根是( )
| A. | 16 | B. | 4 | C. | -4 | D. | ±4 |
1.将100个数据分成①~⑧组,如表所示:
那么第④组的频数为24.
| 编号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ |
| 频数 | 4 | 8 | 12 |  | 24 | 18 | 7 | 3 |
11. 如图,∠ACB=90°,CD⊥AB于D,能表示点到直线的距离的线段有( )
如图,∠ACB=90°,CD⊥AB于D,能表示点到直线的距离的线段有( )
 如图,∠ACB=90°,CD⊥AB于D,能表示点到直线的距离的线段有( )
如图,∠ACB=90°,CD⊥AB于D,能表示点到直线的距离的线段有( )| A. | 2条 | B. | 3条 | C. | 4条 | D. | 5条 |
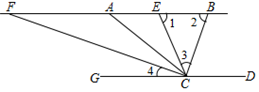 如图,CD∥AB,BC平分∠ACD,CF平分∠ACG,
如图,CD∥AB,BC平分∠ACD,CF平分∠ACG,
 如图,AB是⊙O的直径,点C在⊙O上,OD∥AC,交BC于D.若BD=1,则BC的长为2.
如图,AB是⊙O的直径,点C在⊙O上,OD∥AC,交BC于D.若BD=1,则BC的长为2.