题目内容
设实数x满足|2-x|=2+|x|，则
=（ ）
| (x-3)2 |
| A、x-3 | B、3-x |
| C、±（x-3） | D、3 |
分析：由|2-x|=2+|x|，即可推出①若x＜0，|2-x|=2+|x|，则
=|x-3|=3-x，②若x＞2，|2-x|=2+|x|，当2＜x＜3时，则
=|x-3|=3-x，当x＞3时，则
=|x-3|=x-3，所以，实数x满足|2-x|=2+|x|，则
=±（x-3）．
| (x-3)2 |
| (x-3)2 |
| (x-3)2 |
| (x-3)2 |
解答：解：∵实数x满足|2-x|=2+|x|，
∴若x＜0，|2-x|=2-x，2+|x|=2-x，
则
=|x-3|=3-x，
故选B．
∴若x＜0，|2-x|=2-x，2+|x|=2-x，
则
| (x-3)2 |
故选B．
点评：本题主要考查二次根式的性质、二次根式的化简，关键在于根据等式求出x的取值范围．
练习册系列答案
一线名师提优试卷系列答案
相关题目
设实数a满足0＜a＜1，则在a2，a，
，
中（ ）
| a |
| 1 |
| a |
A、
| ||
B、a最大，
| ||
C、a2最大，
| ||
| D、a最大，a2最小 |
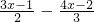
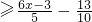，求2|x-1|+|x+4|的最小值
=（ ）