题目内容
设实数a满足0<a<1,则在a2,a,
,
中( )
| a |
| 1 |
| a |
A、
| ||
B、a最大,
| ||
C、a2最大,
| ||
| D、a最大,a2最小 |
分析:可以利用特殊值的方法比较,即可作出判断.
解答:解:利用特殊值法,当x=
时,
=4,x2=
,
=
,
因为:
<
<
<4,则
>
>x>x2,
故
最大,a2最小.
故选A.
| 1 |
| 4 |
| 1 |
| x |
| 1 |
| 16 |
| x |
| 1 |
| 2 |
因为:
| 1 |
| 16 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| x |
| x |
故
| 1 |
| a |
故选A.
点评:本题主要考查了有理数大小的比较,特殊值法是解决选择题的常用方法.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
设实数x满足|2-x|=2+|x|,则
=( )
| (x-3)2 |
| A、x-3 | B、3-x |
| C、±(x-3) | D、3 |
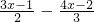
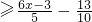 ,求2|x-1|+|x+4|的最小值
,求2|x-1|+|x+4|的最小值 =( )
=( )