题目内容
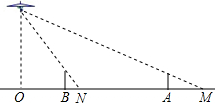 如图,路灯距离地面8.5米,身高1.7米的小军从距离灯的底部(点O)6米的点B处,沿OA所在直线行走至B处14米的A点时,人影长度变长________米.
如图,路灯距离地面8.5米,身高1.7米的小军从距离灯的底部(点O)6米的点B处,沿OA所在直线行走至B处14米的A点时,人影长度变长________米.
3.5
分析:小军在不同的位置时,均可构成两个相似三角形,可利用相似比求人影长度的变化.
解答:设小明在A处时影长为x,B处时影长为y,
则 =
=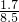 ,
,
∴x=5,
 =
=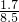 ,
,
∴y=1.5,
∴x-y=3.5,
变长了3.5米.
故答案为3.5米.
点评:此题考查相似三角形对应边成比例,解题的关键是从题目中整理出两对相似三角形并利用相似三角形对应边的比相等求得相应的线段的长.
分析:小军在不同的位置时,均可构成两个相似三角形,可利用相似比求人影长度的变化.
解答:设小明在A处时影长为x,B处时影长为y,
则
 =
=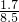 ,
,∴x=5,
 =
=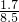 ,
,∴y=1.5,
∴x-y=3.5,
变长了3.5米.
故答案为3.5米.
点评:此题考查相似三角形对应边成比例,解题的关键是从题目中整理出两对相似三角形并利用相似三角形对应边的比相等求得相应的线段的长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长为
如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长为 如图,路灯距离地面8.5米,身高1.7米的小军从距离灯的底部(点O)6米的点B处,沿OA所在直线行走至B处14米的A点时,人影长度变长
如图,路灯距离地面8.5米,身高1.7米的小军从距离灯的底部(点O)6米的点B处,沿OA所在直线行走至B处14米的A点时,人影长度变长

 如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长为 米.
如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长为 米.