��Ŀ����
��ͼ����֪�ھ���ABCD�У�AD=8��CD=4����E�ӵ�D���������߶�DA��ÿ��1����λ�����ٶ����A�����ƶ���ͬʱ��F�ӵ�C������������CD������ÿ��2����λ�����ٶ��ƶ�����B ��E��F���㹲��ʱ������ͬʱֹͣ�˶������E�ƶ���ʱ��Ϊt���룩��
��E��F���㹲��ʱ������ͬʱֹͣ�˶������E�ƶ���ʱ��Ϊt���룩����1����tΪ��ֵʱ������ͬʱֹͣ�˶���
��2�����ı���BCFE�����ΪS����S��t֮��ĺ�����ϵʽ����д��t��ȡֵ��Χ��
��3����tΪ��ֵʱ����E��F��C����Ϊ������������ǵ��������Σ�
��4����tΪ��ֵʱ����BEC=��BFC��
��������1��B��E��F���㹲��ʱ�������FED�ס�FBC������г�������Եó�����t�ı���ʽ�����t��ֵ��
��2����S��t֮��ĺ�����ϵʽ�����Խ��ı���BCFE������ֳ�S��BCE��S��BCF�����֣���ϣ�1��ȷ��t��ȡֵ��Χ��
��3�����ݵ��������ε����ʣ���EF=EC��EC=FC��EF=FC����������ۣ�
��4����BEC=��BFC������ת��Ϊ��BEC=��BCE����BE=BC���ó�����t�ķ��̣����ֵ��
��2����S��t֮��ĺ�����ϵʽ�����Խ��ı���BCFE������ֳ�S��BCE��S��BCF�����֣���ϣ�1��ȷ��t��ȡֵ��Χ��
��3�����ݵ��������ε����ʣ���EF=EC��EC=FC��EF=FC����������ۣ�
��4����BEC=��BFC������ת��Ϊ��BEC=��BCE����BE=BC���ó�����t�ķ��̣����ֵ��
���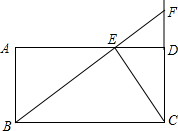 �⣺��1����B��E��F���㹲��ʱ������ͬʱֹͣ�˶�����ͼ��ʾ����1�֣�
�⣺��1����B��E��F���㹲��ʱ������ͬʱֹͣ�˶�����ͼ��ʾ����1�֣�
�������֪��ED=t��BC=8��FD=2t-4��FC=2t��
��ED��BC��
���FED�ס�FBC��
��
=
��
��
=
��
���t=4��
�൱t=4ʱ������ͬʱֹͣ�˶�����3�֣�
��2����ED=t��CF=2t��
��S=S��BCE+S��ECF=
��8��4+
��2t��t=16+t2��
��S=16+t2����0��t��4������6�֣�
��3������EF=ECʱ�����Fֻ����CD���ӳ����ϣ�
��EF2=��2t-4��2+t2=5t2-16t+16��
EC2=42+t2=t2+16��
��5t2-16t+16=t2+16��
��t=4��t=0����ȥ����
����EC=FCʱ��
��EC2=42+t2=t2+16��FC2=4t2��
��t2+16=4t2
����t=
��
����EF=FCʱ��
��EF2=��2t-4��2+t2=5t2-16t+16��FC2=4t2��
��5t2-16t+16=4t2��
��t1=8+4
����ȥ����t2=8-4
��
�൱t��ֵΪ4��
��8-4
ʱ����E��F��C����Ϊ������������ǵ��������Σ���9�֣�
��4����Rt��BCF��Rt��CDE��
�ߡ�BCF=��CDE=90�㣬
=
=2��
��Rt��BCF��Rt��CDE��
���BFC=��CED�� ��10�֣�
��AD��BC��
���BCE=��CED������BEC=��BFC�����BEC=��BCE����BE=BC��
��BE2=t2-16t+80��
��t2-16t+80=64��
��t1=8+4
����ȥ����t2=8-4
��
�൱t=8-4
ʱ����BEC=��BFC�� ��12�֣�
 �⣺��1����B��E��F���㹲��ʱ������ͬʱֹͣ�˶�����ͼ��ʾ����1�֣�
�⣺��1����B��E��F���㹲��ʱ������ͬʱֹͣ�˶�����ͼ��ʾ����1�֣��������֪��ED=t��BC=8��FD=2t-4��FC=2t��
��ED��BC��
���FED�ס�FBC��
��
| FD |
| FC |
| ED |
| BC |
��
| 2t-4 |
| 2t |
| t |
| 8 |
���t=4��
�൱t=4ʱ������ͬʱֹͣ�˶�����3�֣�
��2����ED=t��CF=2t��
��S=S��BCE+S��ECF=
| 1 |
| 2 |
| 1 |
| 2 |
��S=16+t2����0��t��4������6�֣�
��3������EF=ECʱ�����Fֻ����CD���ӳ����ϣ�
��EF2=��2t-4��2+t2=5t2-16t+16��
EC2=42+t2=t2+16��
��5t2-16t+16=t2+16��
��t=4��t=0����ȥ����
����EC=FCʱ��
��EC2=42+t2=t2+16��FC2=4t2��
��t2+16=4t2
����t=
| 4 |
| 3 |
| 3 |
����EF=FCʱ��
��EF2=��2t-4��2+t2=5t2-16t+16��FC2=4t2��
��5t2-16t+16=4t2��
��t1=8+4
| 3 |
| 3 |
�൱t��ֵΪ4��
| 4 |
| 3 |
| 3 |
| 3 |
��4����Rt��BCF��Rt��CDE��
�ߡ�BCF=��CDE=90�㣬
| BC |
| CD |
| CF |
| ED |
��Rt��BCF��Rt��CDE��
���BFC=��CED�� ��10�֣�
��AD��BC��
���BCE=��CED������BEC=��BFC�����BEC=��BCE����BE=BC��
��BE2=t2-16t+80��
��t2-16t+80=64��
��t1=8+4
| 3 |
| 3 |
�൱t=8-4
| 3 |
�������������ν�ϣ��ۺ��Խ�ǿ�����г�����������л������ϣ���һ����˼ά������

��ϰ��ϵ�д�
 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д�
�����Ŀ
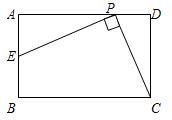 ��ѡ�⣺
��ѡ�⣺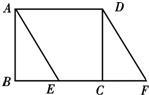 ��ͼ����֪�ھ���ABCD�У�AB=3����E��BC���ҡ�BAE=30�㣬�ӳ�BC����FʹCF=BE������DF��
��ͼ����֪�ھ���ABCD�У�AB=3����E��BC���ҡ�BAE=30�㣬�ӳ�BC����FʹCF=BE������DF��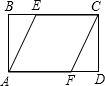 ��ͼ����֪�ھ���ABCD�У�AB=2��BC=4���ı���AFCEΪ���Σ������ε������
��ͼ����֪�ھ���ABCD�У�AB=2��BC=4���ı���AFCEΪ���Σ������ε������ ��ͼ����֪�ھ���ABCD�У�AB=6��BC=8����E�͡�F�ֱ��ǡ�ABC�͡�ADC������Բ����Խ���AC�ֱ�����E��F����EF=
��ͼ����֪�ھ���ABCD�У�AB=6��BC=8����E�͡�F�ֱ��ǡ�ABC�͡�ADC������Բ����Խ���AC�ֱ�����E��F����EF=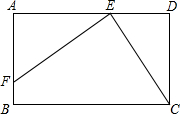 E=3cm��BC=7cm��
E=3cm��BC=7cm��