题目内容
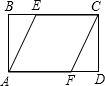 如图,已知在矩形ABCD中,AB=2,BC=4,四边形AFCE为菱形,求菱形的面积.
如图,已知在矩形ABCD中,AB=2,BC=4,四边形AFCE为菱形,求菱形的面积.
分析:首先由菱形的四条边都相等与矩形的四个角是直角,即可得到直角三角形ABE中三边的关系,借助于方程即可求得菱形的边长,则可求得其面积.
解答:解:∵四边形AFCE为菱形,
∴AF=CF=EC=AE,
∵四边形ABCD是矩形,
∴∠B=90°,
设AE=x,则BE=BC-EC=4-x,
∵在Rt△ABE中,AB2+BE2=AE2,
即:22+(4-x)2=x2,
∴x=
,
∴S菱形AFCE=EC•AB=
×2=5.
∴菱形的面积为5.
∴AF=CF=EC=AE,
∵四边形ABCD是矩形,
∴∠B=90°,
设AE=x,则BE=BC-EC=4-x,
∵在Rt△ABE中,AB2+BE2=AE2,
即:22+(4-x)2=x2,
∴x=
| 5 |
| 2 |
∴S菱形AFCE=EC•AB=
| 5 |
| 2 |
∴菱形的面积为5.
点评:此题考查了菱形与矩形的性质,以及直角三角形中的勾股定理.解此题的关键是注意数形结合思想与方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 自选题:
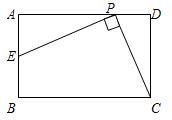
自选题: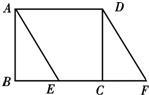 如图,已知在矩形ABCD中,AB=3,点E在BC上且∠BAE=30°,延长BC到点F使CF=BE,连接DF.
如图,已知在矩形ABCD中,AB=3,点E在BC上且∠BAE=30°,延长BC到点F使CF=BE,连接DF. 如图,已知在矩形ABCD中,AB=6,BC=8,⊙E和⊙F分别是△ABC和△ADC的内切圆,与对角线AC分别切于E、F,则EF=
如图,已知在矩形ABCD中,AB=6,BC=8,⊙E和⊙F分别是△ABC和△ADC的内切圆,与对角线AC分别切于E、F,则EF=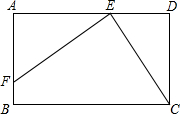 E=3cm,BC=7cm.
E=3cm,BC=7cm.