题目内容
如图①,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC与点D.
(1)当∠B=45°,∠C=75°时,求∠EFD的度数;
(2)通过(1)的运算,你能猜想出∠EFD、∠C、∠B之间数量关系,请直接写出答案
(3)当点F在AE的延长线上时,如图②,其余条件不变,上述结论还成立吗?为什么?
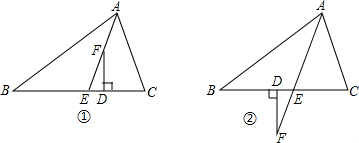
(1)当∠B=45°,∠C=75°时,求∠EFD的度数;
(2)通过(1)的运算,你能猜想出∠EFD、∠C、∠B之间数量关系,请直接写出答案
(3)当点F在AE的延长线上时,如图②,其余条件不变,上述结论还成立吗?为什么?

考点:三角形的外角性质,三角形内角和定理,角平分线的性质
专题:
分析:(1)根据三角形的内角和定理求出∠BAC,再根据角平分线的定义求出∠BAE,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解;
(2)根据三角形的内角和定理和角平分线的定义表示出∠BAE,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠AEC,然后根据直角三角形两锐角互余列式整理即可得解;
(3)结论仍然成立.根据(2)可以得到∠AEC=90°+
(∠B-∠C),根据对顶角相等即可求得∠DEF,然后利用直角三角形的两个锐角互余即可求解.
(2)根据三角形的内角和定理和角平分线的定义表示出∠BAE,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠AEC,然后根据直角三角形两锐角互余列式整理即可得解;
(3)结论仍然成立.根据(2)可以得到∠AEC=90°+
| 1 |
| 2 |
解答:解:(1)∵∠C=75°,∠B=45°,
∴∠BAC=180°-∠C-∠B=180°-75°-45°=60°,
∵AE平分∠BAC,
∴∠BAE=
∠BAC=
×60°=30°,
由三角形的外角性质得,∠AEC=∠B+∠BAE=45°+30°=75°;

(2)由三角形的内角和定理得,∠BAC=180°-∠C-∠B,
∵AE平分∠BAC,
∴∠BAE=
∠BAC=
(180°-∠C-∠B),
由三角形的外角性质得,∠AEC=∠B+∠BAE=∠B+
(180°-∠C-∠B)=90°+
(∠B-∠C),
∵FD⊥BC,
∴∠EFD=90°-∠AEC=90°-90°-
(∠B-∠C)=
(∠C-∠B),
即∠EFD=
(∠C-∠B);
(3)结论∠EFD=
(∠C-∠B)仍然成立.
同(2)可证:∠AEC=90°+
(∠B-∠C),
∴∠DEF=∠AEC=90°+
(∠B-∠C),
∴∠EFD=90°-[90°+
(∠B-∠C)]
=
(∠C-∠B).
∴∠BAC=180°-∠C-∠B=180°-75°-45°=60°,
∵AE平分∠BAC,
∴∠BAE=
| 1 |
| 2 |
| 1 |
| 2 |
由三角形的外角性质得,∠AEC=∠B+∠BAE=45°+30°=75°;

(2)由三角形的内角和定理得,∠BAC=180°-∠C-∠B,
∵AE平分∠BAC,
∴∠BAE=
| 1 |
| 2 |
| 1 |
| 2 |
由三角形的外角性质得,∠AEC=∠B+∠BAE=∠B+
| 1 |
| 2 |
| 1 |
| 2 |
∵FD⊥BC,
∴∠EFD=90°-∠AEC=90°-90°-
| 1 |
| 2 |
| 1 |
| 2 |
即∠EFD=
| 1 |
| 2 |
(3)结论∠EFD=
| 1 |
| 2 |
同(2)可证:∠AEC=90°+
| 1 |
| 2 |
∴∠DEF=∠AEC=90°+
| 1 |
| 2 |
∴∠EFD=90°-[90°+
| 1 |
| 2 |
=
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,要注意整体思想的利用.

练习册系列答案
相关题目
下列计算中,正确的是( )
| A、a2•a3=a6 |
| B、a6÷a2=a3 |
| C、(2a2b)2=2a4b2 |
| D、(a3b)2=a6b2 |
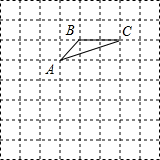 在方格纸上任意连接不在同一直线上的三个格点,便可画出一个三角形.请用这种方式在如下的方格纸上画出两个大小不等的三角形,要求这两个三角形都与格点三角形△ABC相似,且相似比不为1.
在方格纸上任意连接不在同一直线上的三个格点,便可画出一个三角形.请用这种方式在如下的方格纸上画出两个大小不等的三角形,要求这两个三角形都与格点三角形△ABC相似,且相似比不为1.
