题目内容
 如图,直线y=kx+b与坐标轴分别交于A(5,0)、B(0,3)两点,则不等式-kx-b<0的解集为
如图,直线y=kx+b与坐标轴分别交于A(5,0)、B(0,3)两点,则不等式-kx-b<0的解集为
- A.x>5
- B.x<5
- C.x>3
- D.x<0
B
分析:求-kx-b<0的解集,即为kx+b>0,就是求函数值大于0时,x的取值范围.
解答:∵要求-kx-b<0的解集,即为求kx+b>0的解集,
∴从图象上可以看出等y>0时,x<5.
故选:B.
点评:本题考查了一次函数的性质,解题时应结合函数和不等式的关系找出正确的答案.
分析:求-kx-b<0的解集,即为kx+b>0,就是求函数值大于0时,x的取值范围.
解答:∵要求-kx-b<0的解集,即为求kx+b>0的解集,
∴从图象上可以看出等y>0时,x<5.
故选:B.
点评:本题考查了一次函数的性质,解题时应结合函数和不等式的关系找出正确的答案.

练习册系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
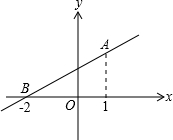 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为