题目内容
求下列各式中的x．
①8x3+27=0；
②
．
解：①∵8x3+27=0，
∴8x3=-27，
∴x3=-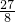
，
解得：x=-
；
②∵
（x-3）2-1=74，
∴（x-3）2=75，
∴（x-3）2=225，
解得：x-3=±15，
解得：x=18或x=-12．
分析：①首先移项，再系数化1，然后利用立方根的定义求解即可求得答案；
②首先移项，再系数化1，可得（x-3）2=225，然后由平方根的定义求解即可求得答案．
点评：此题考查了平方根与立方根的定义．此题比较简单，注意掌握整体思想的应用．
∴8x3=-27，
∴x3=-
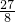，解得：x=-
；②∵
（x-3）2-1=74，∴
（x-3）2=75，∴（x-3）2=225，
解得：x-3=±15，
解得：x=18或x=-12．
分析：①首先移项，再系数化1，然后利用立方根的定义求解即可求得答案；
②首先移项，再系数化1，可得（x-3）2=225，然后由平方根的定义求解即可求得答案．
点评：此题考查了平方根与立方根的定义．此题比较简单，注意掌握整体思想的应用．
练习册系列答案
相关题目