题目内容
如图,在半径为5的⊙O中,点A、B在⊙O中,∠AOB=90°,点C是 的一个动点,AC与OB的延长线相交于点D,设AC=x,BD=y.
的一个动点,AC与OB的延长线相交于点D,设AC=x,BD=y.(1)当x=2时,求y的值;
(2)求y关于x的函数解析式;
(3)如果⊙O1与⊙O相交于点A、C,且⊙O1与⊙O的圆心距为2,当BD=
 OB时,求⊙O1的半径;
OB时,求⊙O1的半径;(4)是否存在点C,使得CD2=DB•DO成立,如果存在,请证明;如果不存在,请简要说明理由.

【答案】分析:(1)过⊙O的圆心作OE⊥AC,垂足为E.通过证明△ODE∽△AOE求得 =
= ,然后将相关线段的长度代入求得y的值;
,然后将相关线段的长度代入求得y的值;
(2)过⊙O的圆心作OE⊥AC,垂足为E.通过证明△ODE∽△AOE求得 =
= ,然后将相关线段的长度代入求得y关于x的函数解析式,再由函数的性质求其定义域;
,然后将相关线段的长度代入求得y关于x的函数解析式,再由函数的性质求其定义域;
(3)当BD= OB时,根据(1)的函数关系式求得y=
OB时,根据(1)的函数关系式求得y= ,x=6.分两种情况来解答O1A的值①当点O1在线段OE上时,O1E=OE-OO1=2;②当点O1在线段EO的延长线上时,O1E=OE+OO1=6,进而求出即可;
,x=6.分两种情况来解答O1A的值①当点O1在线段OE上时,O1E=OE-OO1=2;②当点O1在线段EO的延长线上时,O1E=OE+OO1=6,进而求出即可;
(4)当点C为AB的中点时,∠BOC=∠AOC= ∠AOB=45°,∠OCA=∠OCB=
∠AOB=45°,∠OCA=∠OCB= =67.5°,然后由三角形的内角和定理求得∠DCB=45°,由等量代换求得∠DCB=∠BOC.根据相似三角形的判定定理AA证明△DCB∽△DOC.
=67.5°,然后由三角形的内角和定理求得∠DCB=45°,由等量代换求得∠DCB=∠BOC.根据相似三角形的判定定理AA证明△DCB∽△DOC.
解答: (1)解:如图1,过⊙O的圆心作OE⊥AC,垂足为E,
(1)解:如图1,过⊙O的圆心作OE⊥AC,垂足为E,
∴AE= AC=1,OE=
AC=1,OE= =2
=2 .
.
∵∠DEO=∠AOB=90°,∴∠D=90°-∠EOD=∠AOE,
∴△ODE∽△AOE.
∴ =
= ,
,
∵OD=y+5,
∴ =
= ,
,
解得:y=10 -5;
-5;
(2)解:如图1,过⊙O的圆心作OE⊥AC,垂足为E,
∴AE= AC=
AC= x,OE=
x,OE= =
= .
.
∵∠DEO=∠AOB=90°,
∴∠D=90°-∠EOD=∠AOE,
∴△ODE∽△AOE.
∴ =
= ,
,
∵OD=y+5,
∴ =
= .
.
∴y关于x的函数解析式为:
y= ,定义域为:0<x<5
,定义域为:0<x<5 .
.
(3)解:如图2,当BD= OB时,
OB时,
则y= ,
,
即 =
= ,
,
∴解得:x=6.
∴AE= x=3,OE=
x=3,OE= =4.
=4.
当点O1在线段OE上时,
O1E=OE-OO1=2,
O1A= =
= =
= .
.
当点O1在线段EO的延长线上时,O1E=OE+OO1=6,
O1A= =
= =
= .
.
∴⊙O1的半径为 或3
或3 .
.
(4)存在,当点C为 的中点时,△DCB∽△DOC.
的中点时,△DCB∽△DOC.
证明:∵当点C为 的中点时,∠BOC=∠AOC=
的中点时,∠BOC=∠AOC= ∠AOB=45°,
∠AOB=45°,
又∵OA=OC=OB,
∴∠OCA=∠OCB= =67.5°,
=67.5°,
∴∠DCB=180°-∠OCA-∠OCB=45°.
∴∠DCB=∠BOC.
又∵∠D=∠D,
∴△DCB∽△DOC.
∴存在点C,使得△DCB∽△DOC.
点评:本题主要考查了圆与圆的位置关系、勾股定理.此题很复杂,解答此题的关键是作出辅助线OE⊥AC,利用相似三角形的判定定理及性质解答,解答(3)时注意分两种情况讨论,不要漏解.
 =
= ,然后将相关线段的长度代入求得y的值;
,然后将相关线段的长度代入求得y的值;(2)过⊙O的圆心作OE⊥AC,垂足为E.通过证明△ODE∽△AOE求得
 =
= ,然后将相关线段的长度代入求得y关于x的函数解析式,再由函数的性质求其定义域;
,然后将相关线段的长度代入求得y关于x的函数解析式,再由函数的性质求其定义域;(3)当BD=
 OB时,根据(1)的函数关系式求得y=
OB时,根据(1)的函数关系式求得y= ,x=6.分两种情况来解答O1A的值①当点O1在线段OE上时,O1E=OE-OO1=2;②当点O1在线段EO的延长线上时,O1E=OE+OO1=6,进而求出即可;
,x=6.分两种情况来解答O1A的值①当点O1在线段OE上时,O1E=OE-OO1=2;②当点O1在线段EO的延长线上时,O1E=OE+OO1=6,进而求出即可;(4)当点C为AB的中点时,∠BOC=∠AOC=
 ∠AOB=45°,∠OCA=∠OCB=
∠AOB=45°,∠OCA=∠OCB= =67.5°,然后由三角形的内角和定理求得∠DCB=45°,由等量代换求得∠DCB=∠BOC.根据相似三角形的判定定理AA证明△DCB∽△DOC.
=67.5°,然后由三角形的内角和定理求得∠DCB=45°,由等量代换求得∠DCB=∠BOC.根据相似三角形的判定定理AA证明△DCB∽△DOC.解答:
 (1)解:如图1,过⊙O的圆心作OE⊥AC,垂足为E,
(1)解:如图1,过⊙O的圆心作OE⊥AC,垂足为E,∴AE=
 AC=1,OE=
AC=1,OE= =2
=2 .
.∵∠DEO=∠AOB=90°,∴∠D=90°-∠EOD=∠AOE,
∴△ODE∽△AOE.
∴
 =
= ,
,∵OD=y+5,
∴
 =
= ,
,解得:y=10
 -5;
-5;(2)解:如图1,过⊙O的圆心作OE⊥AC,垂足为E,
∴AE=
 AC=
AC= x,OE=
x,OE= =
= .
.∵∠DEO=∠AOB=90°,
∴∠D=90°-∠EOD=∠AOE,
∴△ODE∽△AOE.
∴
 =
= ,
,∵OD=y+5,
∴
 =
= .
.∴y关于x的函数解析式为:
y=
 ,定义域为:0<x<5
,定义域为:0<x<5 .
.(3)解:如图2,当BD=
 OB时,
OB时,
则y=
 ,
,即
 =
= ,
,∴解得:x=6.
∴AE=
 x=3,OE=
x=3,OE= =4.
=4.当点O1在线段OE上时,
O1E=OE-OO1=2,
O1A=
 =
= =
= .
.当点O1在线段EO的延长线上时,O1E=OE+OO1=6,
O1A=
 =
= =
= .
.∴⊙O1的半径为
 或3
或3 .
.(4)存在,当点C为
 的中点时,△DCB∽△DOC.
的中点时,△DCB∽△DOC.证明:∵当点C为
 的中点时,∠BOC=∠AOC=
的中点时,∠BOC=∠AOC= ∠AOB=45°,
∠AOB=45°,又∵OA=OC=OB,
∴∠OCA=∠OCB=
 =67.5°,
=67.5°,∴∠DCB=180°-∠OCA-∠OCB=45°.
∴∠DCB=∠BOC.
又∵∠D=∠D,
∴△DCB∽△DOC.
∴存在点C,使得△DCB∽△DOC.
点评:本题主要考查了圆与圆的位置关系、勾股定理.此题很复杂,解答此题的关键是作出辅助线OE⊥AC,利用相似三角形的判定定理及性质解答,解答(3)时注意分两种情况讨论,不要漏解.

练习册系列答案
相关题目
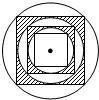 如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )
如图,在半径为R的圆内作一个内接正方形,然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是( )A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
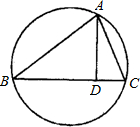 如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为
如图,在半径为R的圆中作一内接△ABC,使BC边上的高AD=h(定值),这样的三角形可作出无数个,但AB•AC为定值,其值为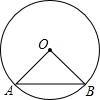 如图,在半径为2的⊙O中,弦AB的长为2
如图,在半径为2的⊙O中,弦AB的长为2 (2012•陕西)如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( )
(2012•陕西)如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为( ) (2013•上海模拟)如图,在半径为1的扇形AOB中,∠AOB=90°,点P是
(2013•上海模拟)如图,在半径为1的扇形AOB中,∠AOB=90°,点P是