题目内容
如图所示，△ABC中，AB=5，AC=9，则BC边上的中线AD的取值范围是（ ）| A、4＜AD＜14 | B、0＜AD＜14 | C、2＜AD＜7 | D、5＜AD＜9 |
分析：此题通过辅助线，即倍长中线．巧妙构造全等三角形，把要求的线段和已知的线段转换到一个三角形中，根据三角形的三边关系进行分析求解．
解答：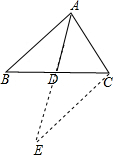
解：如图，延长AD到E，使DE=AD，连接CE，
∵点D是中点，
∴BD=CD
又∠ADB=∠CDE
∴△ABD≌△EDC
∴CE=AB
根据三角形的三边关系，得：（AC-CE）＜AE＜（AC+CE）
即4＜AE＜14
而AD=
AE
∴2＜AD＜7．
故选C．
解：如图，延长AD到E，使DE=AD，连接CE，∵点D是中点，
∴BD=CD
又∠ADB=∠CDE
∴△ABD≌△EDC
∴CE=AB
根据三角形的三边关系，得：（AC-CE）＜AE＜（AC+CE）
即4＜AE＜14
而AD=
| 1 |
| 2 |
∴2＜AD＜7．
故选C．
点评：本题通过作辅助线，构造全等三角形，把AB转移为CE，再利用三角形中三边的关系求解．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，△ABC中，AB=AC，∠BAC=120°，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．
16、如图所示，△ABC中，∠C=90°，DE垂直平分斜边AB，分别交AB、AC于D、E，∠CAE：∠EAB=5：2，则∠B=
如图所示，△ABC中，AB=AC=10，BD是AC边的高线，DC=2，试求BD的长．
如图所示，△ABC中，BC的垂直平分线交AB于点E，若△ABC的周长为10，BC=4，则△ACE的周长是
如图所示，△ABC中，AB=AC，BD⊥AC，垂足为D，求∠DBC与∠A的关系．