题目内容
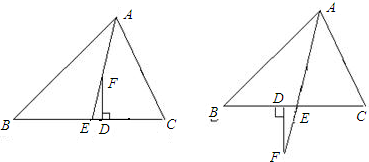
在三角形ABC中,AE平分∠ABC,∠C>∠B,且FD⊥BC于D点.
(1)试推出∠EFD,∠B,∠C的关系;
(2)当点F在AE的延长线上时,其余条件不变,你在题(1)推导的结论还成立吗?说明理由.
解:(1)∠EFD= ∠C-
∠C- ∠B,理由如下:
∠B,理由如下:
由三角形的外角性质知:∠FED=∠B+ ∠BAC,
∠BAC,
故∠B+ ∠BAC+∠EFD=90°;①
∠BAC+∠EFD=90°;①
△ABC中,由三角形内角和定理得:
∠B+∠BAC+∠C=180°,
即: ∠C+
∠C+ ∠B+
∠B+ ∠BAC=90°,②
∠BAC=90°,②
②-①,得:
∠EFD= ∠C-
∠C- ∠B.
∠B.
(2)成立.理由与(1)相同.
分析:(1)在△EFD中,由三角形的外角性质知:∠FED=∠B+ ∠BAC,所以∠B+
∠BAC,所以∠B+ ∠BAC+∠EFD=90°,联立△ABC中,由三角形内角和定理得到的式子,即可推出∠EFD,∠B,∠C的关系.
∠BAC+∠EFD=90°,联立△ABC中,由三角形内角和定理得到的式子,即可推出∠EFD,∠B,∠C的关系.
(2)思路和解法与(1)完全相同.
点评:此题考查的知识点有:三角形内角和定理、三角形的外角性质以及角平分线的定义,难度不大.
 ∠C-
∠C- ∠B,理由如下:
∠B,理由如下:由三角形的外角性质知:∠FED=∠B+
 ∠BAC,
∠BAC,故∠B+
 ∠BAC+∠EFD=90°;①
∠BAC+∠EFD=90°;①△ABC中,由三角形内角和定理得:
∠B+∠BAC+∠C=180°,
即:
 ∠C+
∠C+ ∠B+
∠B+ ∠BAC=90°,②
∠BAC=90°,②②-①,得:
∠EFD=
 ∠C-
∠C- ∠B.
∠B.(2)成立.理由与(1)相同.
分析:(1)在△EFD中,由三角形的外角性质知:∠FED=∠B+
 ∠BAC,所以∠B+
∠BAC,所以∠B+ ∠BAC+∠EFD=90°,联立△ABC中,由三角形内角和定理得到的式子,即可推出∠EFD,∠B,∠C的关系.
∠BAC+∠EFD=90°,联立△ABC中,由三角形内角和定理得到的式子,即可推出∠EFD,∠B,∠C的关系.(2)思路和解法与(1)完全相同.
点评:此题考查的知识点有:三角形内角和定理、三角形的外角性质以及角平分线的定义,难度不大.

练习册系列答案
相关题目
 22、如图,在三角形ABC中,AB=AC=BD,AD=CD,则∠B=
22、如图,在三角形ABC中,AB=AC=BD,AD=CD,则∠B= 20、如图,在三角形ABC中,BD平分∠ABC,∠1=∠3,求证:∠ADE=∠C.
20、如图,在三角形ABC中,BD平分∠ABC,∠1=∠3,求证:∠ADE=∠C. 如图,在三角形ABC中,若AB=AC,BD=BC,若∠ABD=30°,则∠A的大小是
如图,在三角形ABC中,若AB=AC,BD=BC,若∠ABD=30°,则∠A的大小是