题目内容
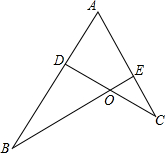如图，给出三个等式：①| AB |
| AC |
| AE |
| AD |
分析：这是一道开放性的题，已知为角和边的比值关系，由此可想到根据相似三角形的判定方法进行适当的组合．
解答：解：命题：
（1）若①
=
，则②OB•OE=OC•OD，③∠B=∠C．
或（2）若②OB•OE=OC•OD，则①
=
，③∠B=∠C．
或（3）若③∠B=∠C，则①
=
，②OB•OE=OC•OD．
以第一个命题为例证明如下：
∵
=
，∠A=∠A，
∴△ABE∽△ACD．
∴∠B=∠C．
又∵∠BOD=∠COE，
∴△BOD∽△COE．
∴
=
．
即OB•OE=OC•OD．
（1）若①
| AB |
| AC |
| AE |
| AD |
或（2）若②OB•OE=OC•OD，则①
| AB |
| AC |
| AE |
| AD |
或（3）若③∠B=∠C，则①
| AB |
| AC |
| AE |
| AD |
以第一个命题为例证明如下：
∵
| AB |
| AC |
| AE |
| AD |
∴△ABE∽△ACD．
∴∠B=∠C．
又∵∠BOD=∠COE，
∴△BOD∽△COE．
∴
| OB |
| OC |
| OD |
| OE |
即OB•OE=OC•OD．
点评：本题主要考查了相似三角形的判定定理的熟练运用．
练习册系列答案
相关题目
23、如图，给出四个等式：①AE=AD；②AB=AC；③OB=OC：④∠B=∠C．现请你选取其中的三个，以某两个作为已知条件，另一个作为结论．
21、如图，给出四个等式：①AE=AD；②AB=AC；③OB=OC；④∠B=∠C． 现选取其中的三个，以两个作为已知条件，另一个作为结论组成命题．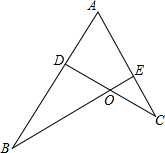
如图，给出三个等式：①
=
；②OB•OE=OC•OD；③∠B=∠C．现选取其中的一个作为已知条件，另两个作为结论，请你写出一个正确的命题，并加以证明．
=
；②OB•OE=OC•OD；③∠B=∠C．现选取其中的一个作为已知条件，另两个作为结论，请你写出一个正确的命题，并加以证明．