题目内容
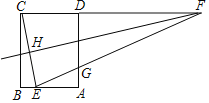
【题目】如图，矩形ABCD中，AB＝3，AD＝4，E在AB上，AE＝2，HF是CE的垂直平分线，交CD的延长线于点F，连结EF交AD于点G，则
的值是（ ）
A.
B.
C.
D.
【答案】C
【解析】
先利用勾股定理计算出CE＝
，再利用HF是CE的垂直平分线得到CH＝
，接着证明Rt△FCH∽Rt△CEB，利用相似比计算出FC＝
，所以DF＝
，然后证明△FDG∽△EAG，从而利用相似比可得到
的比值．
解：∵矩形ABCD中，AB＝3，AD＝4，AE＝2，
∴BC＝4，CD＝3，BE＝1，
∴CE＝
＝，
∵HF是CE的垂直平分线，
∴CH＝
CE＝，FH⊥CE，
∵CF∥AB，
∴∠FCH＝∠CEB，
∴Rt△FCH∽Rt△CEB，
∴
，即
＝
，
∴FC＝，
∴DF＝﹣3＝
∵DF∥AE，
∴△FDG∽△EAG，
∴
．
故选：C．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
