题目内容
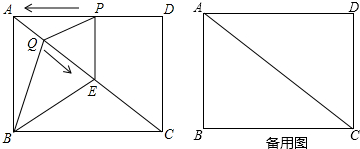
如图,在矩形ABCD中,AB=3,BC=4,动点P从点D出发沿DA向终点A运动,同时动点Q从点A出发沿对角线AC向终点C运动.过点P作PE∥DC,交AC于点E,动点P、Q的运动速度是每秒1个单位长度,运动时间为t秒,当点P运动到点A时,P、Q两点同时停止运动.
(1)用含有t的代数式表示PE= ;
(2)探究:当t为何值时,四边形PQBE为梯形?
(3)是否存在这样的点P和点Q,使△PQE为等腰三角形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.
(1)用含有t的代数式表示PE=
(2)探究:当t为何值时,四边形PQBE为梯形?
(3)是否存在这样的点P和点Q,使△PQE为等腰三角形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.

考点:四边形综合题
专题:
分析:(1)由四边形ABCD为矩形,得到∠D为直角,对边相等,可得三角形ADC为直角三角形,由AD与DC的长,利用勾股定理求出AC的长,再由PE平行于CD,利用两直线平行得到两对同位角相等,可得出三角形APE与三角形ADC相似,由相似得比例,将各自的值代入,整理后得到y与x的关系式;
(2)若QB与PE平行,得到四边形PQBE为矩形,不合题意,故QB与PE不平行,当PQ与BE平行时,利用两直线平行得到一对内错角相等,可得出一对邻补角相等,再由AD与BC平行,得到一对内错角相等,可得出三角形APQ与三角形BEC相似,由相似得比例列出关于x的方程,求出方程的解即可得到四边形PQBE为梯形时x的值;
(3)存在这样的点P和点Q,使P、Q、E为顶点的三角形是等腰三角形,分两种情况考虑:当Q在AE上时,由AE-AQ表示出QE,再根据PQ=PE,PQ=EQ,PE=QE三种情况,分别列出关于x的方程,求出方程的解即可得到满足题意x的值;当Q在EC上时,由AQ-AE表示出QE,此时三角形为钝角三角形,只能PE=QE列出关于x的方程,求出方程的解得到满足题意x的值,综上,得到所有满足题意的x的值.
(2)若QB与PE平行,得到四边形PQBE为矩形,不合题意,故QB与PE不平行,当PQ与BE平行时,利用两直线平行得到一对内错角相等,可得出一对邻补角相等,再由AD与BC平行,得到一对内错角相等,可得出三角形APQ与三角形BEC相似,由相似得比例列出关于x的方程,求出方程的解即可得到四边形PQBE为梯形时x的值;
(3)存在这样的点P和点Q,使P、Q、E为顶点的三角形是等腰三角形,分两种情况考虑:当Q在AE上时,由AE-AQ表示出QE,再根据PQ=PE,PQ=EQ,PE=QE三种情况,分别列出关于x的方程,求出方程的解即可得到满足题意x的值;当Q在EC上时,由AQ-AE表示出QE,此时三角形为钝角三角形,只能PE=QE列出关于x的方程,求出方程的解得到满足题意x的值,综上,得到所有满足题意的x的值.
解答: 解:(1)∵四边形ABCD是矩形,
解:(1)∵四边形ABCD是矩形,
∴∠D=90°,AB=DC=3,AD=BC=4,
∴在Rt△ACD中,利用勾股定理得:AC=
=5,
∵PE∥CD,
∴∠APE=∠ADC,∠AEP=∠ACD,
∴△APE∽△ADC,
又∵PD=t,AD=4,AP=AD-PD=4-t,AC=5,DC=3,
∴
=
=
,即
=
=
,
∴PE=-
t+3.
故答案为:-
t+3;
(2)若QB∥PE,四边形PQBE是矩形,非梯形,
故QB与PE不平行,
当QP∥BE时,
∵∠PQE=∠BEQ,
∴∠AQP=∠CEB,
∵AD∥BC,
∴∠PAQ=∠BCE,
∴△PAQ∽△BCE,
由(1)得:AE=-
t+5,PA=4-t,BC=4,AQ=t,
∴
=
=
,即
=
=
,
整理得:5(4-t)=16,
解得:t=
,
∴当t=
时,QP∥BE,而QB与PE不平行,此时四边形PQBE是梯形;
(3)存在.
分两种情况:
当Q在线段AE上时:QE=AE-AQ=-
t+5-t=5-
t,
(i)当QE=PE时,5-
t=-
t+3,
解得:x=
;
(ii)当QP=QE时,∠QPE=∠QEP,
∵∠APQ+∠QPE=90°,∠PAQ+∠QEP=90°,
∴∠APQ=∠PAQ,
∴AQ=QP=QE,
∴t=5-
t,
解得,t=
;
(iii)当QP=PE时,过P作PF⊥QE于F(如图1),
可得:FE=
QE=
(5-
t)=
,
∵PE∥DC,∴∠AEP=∠ACD,
∴cos∠AEP=cos∠ACD=
=
,
∵cos∠AEP=
=
=
,
解得t=
;
当点Q在线段EC上时,△PQE只能是钝角三角形,如图2所示:
∴PE=EQ=AQ-AE,AQ=t,AE=-
t+5,PE=-
t+3,
∴-
t+3=t-(-
t+5),
解得nt=
.
综上,当t=
或t=
或t=
或t=
时,△PQE为等腰三角形.
 解:(1)∵四边形ABCD是矩形,
解:(1)∵四边形ABCD是矩形,∴∠D=90°,AB=DC=3,AD=BC=4,
∴在Rt△ACD中,利用勾股定理得:AC=
| AC2+CD2 |
∵PE∥CD,
∴∠APE=∠ADC,∠AEP=∠ACD,
∴△APE∽△ADC,
又∵PD=t,AD=4,AP=AD-PD=4-t,AC=5,DC=3,
∴
| AP |
| AD |
| AE |
| AC |
| PE |
| DC |
| 4-t |
| 4 |
| AE |
| 5 |
| PE |
| 3 |
∴PE=-
| 3 |
| 4 |
故答案为:-
| 3 |
| 4 |
(2)若QB∥PE,四边形PQBE是矩形,非梯形,
故QB与PE不平行,
当QP∥BE时,
∵∠PQE=∠BEQ,
∴∠AQP=∠CEB,
∵AD∥BC,
∴∠PAQ=∠BCE,
∴△PAQ∽△BCE,
由(1)得:AE=-
| 5 |
| 4 |
∴
| PA |
| BC |
| AQ |
| CE |
| AQ |
| AC-AE |
| 4-t |
| 4 |
| x | ||
5-(-
|
| 4t |
| 5t |
整理得:5(4-t)=16,
解得:t=
| 4 |
| 5 |
∴当t=
| 4 |
| 5 |
(3)存在.
分两种情况:
当Q在线段AE上时:QE=AE-AQ=-
| 5 |
| 4 |
| 9 |
| 4 |
(i)当QE=PE时,5-
| 9 |
| 4 |
| 3 |
| 4 |
解得:x=
| 4 |
| 3 |
(ii)当QP=QE时,∠QPE=∠QEP,
∵∠APQ+∠QPE=90°,∠PAQ+∠QEP=90°,
∴∠APQ=∠PAQ,
∴AQ=QP=QE,
∴t=5-
| 9 |
| 4 |
解得,t=
| 20 |
| 13 |
(iii)当QP=PE时,过P作PF⊥QE于F(如图1),
可得:FE=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
| 20-9t |
| 8 |
∵PE∥DC,∴∠AEP=∠ACD,
∴cos∠AEP=cos∠ACD=
| CD |
| AC |
| 3 |
| 5 |
∵cos∠AEP=
| EF |
| PE |
| ||
-
|
| 3 |
| 5 |
解得t=
| 28 |
| 27 |
当点Q在线段EC上时,△PQE只能是钝角三角形,如图2所示:
∴PE=EQ=AQ-AE,AQ=t,AE=-
| 5 |
| 4 |
| 3 |
| 4 |
∴-
| 3 |
| 4 |
| 5 |
| 4 |
解得nt=
| 8 |
| 3 |
综上,当t=
| 4 |
| 3 |
| 20 |
| 13 |
| 28 |
| 27 |
| 8 |
| 3 |
点评:此题考查的是四边形综合题,涉及的知识有:矩形的性质,勾股定理,相似三角形的判定与性质,平行线的性质,梯形的判定,以及等腰三角形的性质,利用了数形结合及分类讨论的数学思想,分类讨论时要做到不重不漏,考虑问题要全面.

练习册系列答案
相关题目
如果a>0,b<0,且|a|<|b|,则下列正确的是( )
| A、a+b<0 | B、a+b>0 |
| C、a+b=0 | D、ab=0 |
 如图所示,在矩形ABCD中,两条对角线AC、BD相交于点O,∠AOB=60°,AB=6.
如图所示,在矩形ABCD中,两条对角线AC、BD相交于点O,∠AOB=60°,AB=6.
 如图,有一块直角三角形XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.若在△ABC中∠A=40°,则∠ABX+∠ACX=
如图,有一块直角三角形XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.若在△ABC中∠A=40°,则∠ABX+∠ACX= 如图,在直角坐标系中,点P在x轴上,⊙P于x轴交于A、B两点,与y轴交于C、D两点,抛物线y=ax2+bx+c经过点A、B、C,已知A(-1,0),C(0,-2).
如图,在直角坐标系中,点P在x轴上,⊙P于x轴交于A、B两点,与y轴交于C、D两点,抛物线y=ax2+bx+c经过点A、B、C,已知A(-1,0),C(0,-2).