题目内容
如图,设P到等边三角形ABC两顶点A、B的距离分别为2、3,则PC所能达到的最大值为
- A.

- B.

- C.5
- D.6
C
分析:把PA绕点A逆时针旋转60°,得AD,则DA=PA,连CD,DP,CP,由△ABC为等边三角形ABC,得到∠DAC=∠BAP,AC=AB,于是有∴△DAC≌△PAB,则DC=PB,所以PC≤DP+DC,即可得到PC所能达到的最大值.
解答: 解:把PA绕点A逆时针旋转60°,得AD,则DA=PA,连CD,DP,CP,如图,
解:把PA绕点A逆时针旋转60°,得AD,则DA=PA,连CD,DP,CP,如图,
∵△ABC为等边三角形ABC,
∴∠BAC=60°,AC=AB
∴∠DAC=∠BAP,
∴△DAC≌△PAB,
∴DC=PB,
而PB=3,PA=2,
∴DC=3,
∵PC≤DP+DC,
∴PC≤5,
所以PC所能达到的最大值为5.
故选C.
点评:本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了等边三角形的性质和三角形全等的判定与性质.
分析:把PA绕点A逆时针旋转60°,得AD,则DA=PA,连CD,DP,CP,由△ABC为等边三角形ABC,得到∠DAC=∠BAP,AC=AB,于是有∴△DAC≌△PAB,则DC=PB,所以PC≤DP+DC,即可得到PC所能达到的最大值.
解答:
 解:把PA绕点A逆时针旋转60°,得AD,则DA=PA,连CD,DP,CP,如图,
解:把PA绕点A逆时针旋转60°,得AD,则DA=PA,连CD,DP,CP,如图,∵△ABC为等边三角形ABC,
∴∠BAC=60°,AC=AB
∴∠DAC=∠BAP,
∴△DAC≌△PAB,
∴DC=PB,
而PB=3,PA=2,
∴DC=3,
∵PC≤DP+DC,
∴PC≤5,
所以PC所能达到的最大值为5.
故选C.
点评:本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了等边三角形的性质和三角形全等的判定与性质.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
如图,设P到等边三角形ABC两顶点A、B的距离分别为2、3,则PC所能达到的最大值为( )

A、
| ||
B、
| ||
| C、5 | ||
| D、6 |
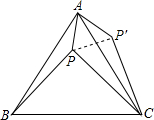 (按课改要求命制)如图,设P是等边三角形ABC内的一点,PA=1,PB=2,PC=
(按课改要求命制)如图,设P是等边三角形ABC内的一点,PA=1,PB=2,PC= ,将△ABP绕点A按逆时针方向旋转,使AB与AC重合,点P旋转到P´外,则sin∠PCP′的值是 (不取近似值).
,将△ABP绕点A按逆时针方向旋转,使AB与AC重合,点P旋转到P´外,则sin∠PCP′的值是 (不取近似值).


