题目内容
(按课改要求命制)如图,设P是等边三角形ABC内的一点,PA=1,PB=2,PC= ,将△ABP绕点A按逆时针方向旋转,使AB与AC重合,点P旋转到P´外,则sin∠PCP′的值是 (不取近似值).
,将△ABP绕点A按逆时针方向旋转,使AB与AC重合,点P旋转到P´外,则sin∠PCP′的值是 (不取近似值).
【答案】分析:根据题意,旋转角度为60°.易证明△APP′是等边三角形,PP′=1;
由CP′=BP=2,PC=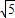 可证明△PCP′是直角三角形,且∠PP′C=90°.
可证明△PCP′是直角三角形,且∠PP′C=90°.
根据三角函数的定义求解.
解答:解:∵△ABC为等边三角形,∴∠BAC=60°.
根据旋转的性质,有
∠PAP′=60°,AP′=AP=1,CP′=BP=2.
∴△APP′是等边三角形,PP′=1.
在△PCP′中,
PC=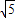 ,PP′=1,CP′=2.
,PP′=1,CP′=2.
∴PC2=P′P2+P′C2.
∴△PCP′是直角三角形,且∠PP′C=90°.
∴sin∠PCP′=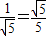 .
.
点评:此题考查了旋转的性质及直角三角形的判定和三角函数等知识点,有一定的综合性.
由CP′=BP=2,PC=
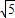 可证明△PCP′是直角三角形,且∠PP′C=90°.
可证明△PCP′是直角三角形,且∠PP′C=90°.根据三角函数的定义求解.
解答:解:∵△ABC为等边三角形,∴∠BAC=60°.
根据旋转的性质,有
∠PAP′=60°,AP′=AP=1,CP′=BP=2.
∴△APP′是等边三角形,PP′=1.
在△PCP′中,
PC=
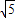 ,PP′=1,CP′=2.
,PP′=1,CP′=2.∴PC2=P′P2+P′C2.
∴△PCP′是直角三角形,且∠PP′C=90°.
∴sin∠PCP′=
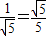 .
.点评:此题考查了旋转的性质及直角三角形的判定和三角函数等知识点,有一定的综合性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
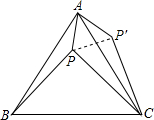 (按课改要求命制)如图,设P是等边三角形ABC内的一点,PA=1,PB=2,PC=
(按课改要求命制)如图,设P是等边三角形ABC内的一点,PA=1,PB=2,PC=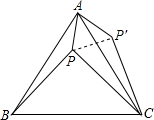
 ,将△ABP绕点A按逆时针方向旋转,使AB与AC重合,点P旋转到P´外,则sin∠PCP′的值是 (不取近似值).
,将△ABP绕点A按逆时针方向旋转,使AB与AC重合,点P旋转到P´外,则sin∠PCP′的值是 (不取近似值).
 ,将△ABP绕点A按逆时针方向旋转,使AB与AC重合,点P旋转到P´外,则sin∠PCP′的值是 (不取近似值).
,将△ABP绕点A按逆时针方向旋转,使AB与AC重合,点P旋转到P´外,则sin∠PCP′的值是 (不取近似值).