Question

【题目】如图，在中，，若是和的平分线交点，求的度数。

若是内任意一点，试探究与之间的关系，并说明理由

请你直接利用以上结论，解决以下问题：

①图中点为内任意一点，若则

②如图平分平分，若，求的度数.

Answer 1

【答案】（1）∠BDC=125°；（2）∠BDC=∠BAC+∠ABD+∠ACD，理由见解析；（3）①60；②∠DCE=90°.

【解析】

（1）根据三角形的内角和与DB平分∠ABC，DC平分∠ACB可求得∠DBC+∠DCB的度数，再在△DBC中应用三角形内角和定理即可求出结果；

（2）作射线AD，再运用三角形的外角性质即可得出结论；

（3）①直接应用（2）的结论计算即可；

②先由（2）的结论求出∠ADB+∠AEB的度数，再由CD平分∠ADB，CE平分∠ACB可求出∠ADC+∠AEC的度数，然后再运用（2）的结论即可求出结果.

解：（1）∵∠A=70°，

∴∠ABC+∠ACB=180°－∠A=180°－70°=110°，

∵DB平分∠ABC，DC平分∠ACB，

∴∠DBC=∠ABC，∠DCB=∠ACB，

∴∠DBC+∠DCB=(∠ABC+∠ACB)=×110°=55°，

∴∠BDC=180°－55°=125°；

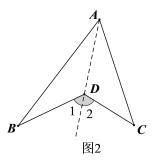
（2）∠BDC=∠BAC+∠ABD+∠ACD，理由如下：

如图2，作射线AD，∵∠1、∠2分别是△ABD和△ACD的外角，

∴∠1=∠BAD+∠ABD，∠2=∠CAD+∠ACD，

∴∠BDC=∠1+∠2=∠BAD+∠ABD+∠CAD+∠ACD=∠BAC+∠ABD+∠ACD.

（3）①由（2）的结论可得：∠ABD+∠ACD=∠BDC―∠A=110°－50°=60°；故答案为60；

②由（2）的结论可得：∠ADB+∠AEB=∠DBE―∠A=130°－50°=80°；

∵CD平分∠ADB，CE平分∠ACB，

∴∠ADC=∠ADB，∠AEC=∠AEB，

∴∠ADC+∠AEC=(∠ADB+∠AEB)=×80°=40°，

又∵∠DCE=∠ADC+∠A+∠AEC，

∴∠DCE=50°+40°=90°.