Question

【题目】已知Rt△ABC的斜边AB在平面直角坐标系的x轴上，点C（1，3）在反比例函数y＝的图象上，且sin∠BAC＝，则点B的坐标为_____.

Answer 1

【答案】（，0）和（﹣，0）．

【解析】

因为A,B两点的位置没有确定，所以存在两种可能，分类讨论，可以利用sin∠BAC＝和C点的坐标，求出A,C两点的横坐标之间的距离和纵坐标之间的距离，还可求出B，C两点的横坐标之间的距离和纵坐标之间的距离，故最后可以写出B点的距离

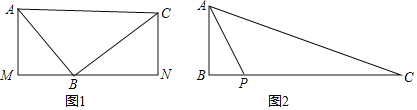
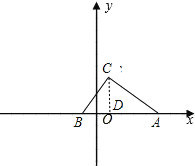
①当点B在点A右边时，如图，

作CD⊥x轴于D．

∵△ABC是直角三角形，

∴∠DAC＝∠DCB，

又∵sin∠BAC＝，

∴tan∠DAC＝，

∴＝，

又∵CD＝3，

∴BD＝，

∴OB＝1+＝，

∴B（，0）；

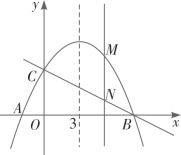
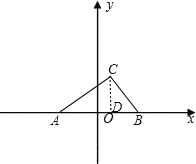
②当点B在点A左边时，如图，

作CD⊥x轴于D．

∵△ABC是直角三角形，

∴∠B+∠A＝90°，∠B+∠BCD＝90°，

∴∠DAC＝∠DCB，

又∵sin∠BAC＝，

∴tan∠DAC＝，

∴＝，

又∵CD＝3，

∴BD＝，

∴OB＝﹣1＝，

∴B（﹣，0），

综上所述：点B的坐标为（，0）和（﹣，0），

故答案为：（ ，0）和（﹣，0）．