题目内容
如图所示，⊙O中弦AB=CD，求证：
．
证明：连接AD，BD，CB，
∵AB=CD，
∴
=
，
∴
=
，
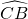∴AD=BC．
分析：连接AD，BD，CB，由在同圆中等弦对等弧可得，弧AB=弧CD，根据等量减上等量还是等量得=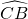，可得AD=BC．
点评：本题利用了在同圆或等圆中，等弧对等弦及等弧对等弦求解．
∵AB=CD，
∴
=，∴
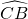=，∴AD=BC．
分析：连接AD，BD，CB，由在同圆中等弦对等弧可得，弧AB=弧CD，根据等量减上等量还是等量得
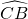=，可得AD=BC．点评：本题利用了在同圆或等圆中，等弧对等弦及等弧对等弦求解．
练习册系列答案
相关题目
如图所示，⊙O中弦AB=CD，求证：
如图所示，⊙O中，弦AC、BD交于E，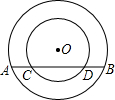
如图所示，同心圆中，大圆的弦AB交小圆于C，D两点，试证明：AC=BD．
．