题目内容
推理填空
如图,已知∠BDG+∠EFG=180°,∠DEF=∠B.试判断∠AED与∠C的大小关系,并说明理由.
解:∠AED=∠C.理由如下:
∵∠EFD+∠EFG=180°﹙ _________ ﹚∠BDG+∠EFG=180°﹙已知﹚
∴∠BDG= _________ ﹙ _________ ﹚
∴BD∥EF﹙ _________ ﹚
∴∠BDE+∠DEF=180°﹙ _________ ﹚
又∵∠DEF=∠B﹙已知﹚
∴∠BDE+∠B=180°﹙ _________ ﹚
∴DE∥BC﹙ _________ ﹚
∴∠AED=∠C﹙ _________ ﹚
如图,已知∠BDG+∠EFG=180°,∠DEF=∠B.试判断∠AED与∠C的大小关系,并说明理由.
解:∠AED=∠C.理由如下:
∵∠EFD+∠EFG=180°﹙ _________ ﹚∠BDG+∠EFG=180°﹙已知﹚
∴∠BDG= _________ ﹙ _________ ﹚
∴BD∥EF﹙ _________ ﹚
∴∠BDE+∠DEF=180°﹙ _________ ﹚
又∵∠DEF=∠B﹙已知﹚
∴∠BDE+∠B=180°﹙ _________ ﹚
∴DE∥BC﹙ _________ ﹚
∴∠AED=∠C﹙ _________ ﹚
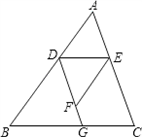
解:∠AED=∠C.理由如下:
∵∠EFD+∠EFG=180°(平角的定义),∠BDG+∠EFG=180°(已知),
∴∠BDG=∠EFD(同角的补角相等),
∴BD∥EF(内错角相等,两直线平行),
∴∠BDE+∠DEF=180°(两直线平行,同旁内角互补),
又∵∠DEF=∠B(已知),
∴∠BDE+∠B=180°(等量代换),
∴DE∥BC(同旁内角互补、两直线平行),
∴∠AED=∠C﹙(两直线平行、同位角相等).
故答案为:平角的定义;∠EFD;同角的补角相等;内错角相等、两直线平行;两直线平行、旁内角互补;等量代换;同旁内角互补、两直线平行;两直线平行、同位角相等.
∵∠EFD+∠EFG=180°(平角的定义),∠BDG+∠EFG=180°(已知),
∴∠BDG=∠EFD(同角的补角相等),
∴BD∥EF(内错角相等,两直线平行),
∴∠BDE+∠DEF=180°(两直线平行,同旁内角互补),
又∵∠DEF=∠B(已知),
∴∠BDE+∠B=180°(等量代换),
∴DE∥BC(同旁内角互补、两直线平行),
∴∠AED=∠C﹙(两直线平行、同位角相等).
故答案为:平角的定义;∠EFD;同角的补角相等;内错角相等、两直线平行;两直线平行、旁内角互补;等量代换;同旁内角互补、两直线平行;两直线平行、同位角相等.

练习册系列答案
相关题目
 24、推理填空
24、推理填空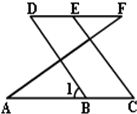 21、推理填空
21、推理填空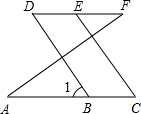 推理填空
推理填空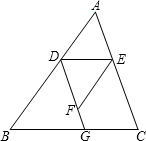 推理填空
推理填空