题目内容
【题目】如图,将一个矩形纸片![]() ,放置在平面直角坐标系中,
,放置在平面直角坐标系中,![]() ,
,![]() 是边
是边![]() 上一点,将
上一点,将![]() 沿直线
沿直线![]() 对折,得到
对折,得到![]() .
.

(1)当![]() 平分
平分![]() 时,求
时,求![]() 的度数和点
的度数和点![]() 的坐标.
的坐标.
(2)连接![]() ,当
,当![]() 时,求
时,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由折叠的性质得:△ANM≌△ADM,由角平分线结合得:∠BAM=∠MAN=∠NAB=30°,由特殊角的三角函数可求DM的长,写出M的坐标;
(2)如图2,作辅助线,构建直角三角形,设NQ=x,则AQ=MQ=1+x,在Rt△ANQ中,由勾股定理列等式可得关于x的方程:(x+1)2=32+x2,求出x,得出AB是AQ的![]() ,即可得出△NAQ和△NAB的关系,得出结论.
,即可得出△NAQ和△NAB的关系,得出结论.
解:(1)![]()
![]()
由折叠得![]()
![]()
![]() 平分
平分![]()
![]()
![]()
![]() 四边形
四边形![]() 是矩形
是矩形
![]()
![]() ,
,
∴AM=2DM,
![]() ,
,
即![]() ,
,
∴![]() ,
,
![]() ;
;
(2)延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接BN,
,连接BN,
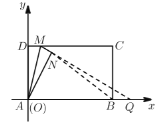
![]() 四边形
四边形![]() 是矩形
是矩形
![]()
![]()
由折叠得![]()
![]()
![]()
![]()
![]()
设![]() ,则
,则![]()
![]()
![]()
在![]() 中,由勾股定理得:
中,由勾股定理得:
![]()
![]() ,解得
,解得![]()
![]()
![]()
![]()
![]()
![]()

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目