题目内容
已知等腰梯形ABCD中，AD∥BC，AB=CD=2cm，BC=5cm，∠A=120°，则它的周长为（ ）
| A、16cm | B、14cm | C、12cm | D、10cm |
分析：利用等腰梯形的性质，矩形的判定与性质，三角形全等的判定与性质，以及直角三角形的边角关系解决．
解答：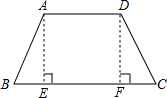
解：如图
过点A、D分别作AE⊥BC，DF⊥BC，垂足分别为E、F，
∴AE∥DF，∠AEF=∠DFE=90°，又AD∥BC，
∴四边形AEFD是矩形，
∴EF=AD，AE=DF，
∵AD∥BC，∠BAD=120°，
∴∠ABE=60°，
在Rt△ABE中，∠BAE=30°，
∴BE=
AB=
×2=1cm，
∵AB=CD，AE=DF，
∴Rt△ABE≌Rt△DCF，
∴CF=BE=1cm，
∴AD=BC-BE-FC=3cm，
∴等腰梯形ABCD的周长=AB+BC+CD+DA=2+5+2+3=12cm．
解：如图过点A、D分别作AE⊥BC，DF⊥BC，垂足分别为E、F，
∴AE∥DF，∠AEF=∠DFE=90°，又AD∥BC，
∴四边形AEFD是矩形，
∴EF=AD，AE=DF，
∵AD∥BC，∠BAD=120°，
∴∠ABE=60°，
在Rt△ABE中，∠BAE=30°，
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=CD，AE=DF，
∴Rt△ABE≌Rt△DCF，
∴CF=BE=1cm，
∴AD=BC-BE-FC=3cm，
∴等腰梯形ABCD的周长=AB+BC+CD+DA=2+5+2+3=12cm．
点评：此题运用的是等腰梯形的性质，矩形的判定与性质，全等三角形的判定．
练习册系列答案
相关题目
3、如图，已知等腰梯形ABCD中，AD∥BC，∠B=60°，AD=2，BC=8，则此等腰梯形的周长为（ ）
如图，已知等腰梯形ABCD的周长是20，AD∥BC，AD＜BC，∠BAD=120°，对角线AC平分∠BCD，则S梯形ABCD=
23、如图所示，已知等腰梯形ABCD中，AD∥BC，AB=CD，点E为梯形外一点，且AE=DE．
如图，已知等腰梯形ABCD中，AB=CD，AD=