题目内容
 如图,一块含有30°角(∠ABC=30°,∠ACB=90°)的木制三角板是由三块宽度相等的木条拼合而成,若木条的宽度为5cm,求制作时拼合缝AA′的长.
如图,一块含有30°角(∠ABC=30°,∠ACB=90°)的木制三角板是由三块宽度相等的木条拼合而成,若木条的宽度为5cm,求制作时拼合缝AA′的长.
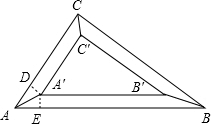 解:过点A′作A′D⊥AC于点D,过点A′作A′E⊥AB于点E
解:过点A′作A′D⊥AC于点D,过点A′作A′E⊥AB于点E∵木制三角板是由三块宽度相等的木条拼合而成
∴A′D=A′E
∴AA′平分∠CAB
∵∠ABC=30°,∠ACB=90°
∴∠CAB=60°
∴∠DAA′=30°
∵∠ADA′=90°
∴DA′=
 AA′
AA′∵木条的宽度为5cm
∴DA′=5cm
∴AA′=10cm.
分析:过点A′作A′D⊥AC于点D,过点A′作A′E⊥AB于点E,易证△AA′D≌△AA′E,则∠DAA′=30°,在直角△AA′D中根据30°角所对的直角边等于斜边的一半就可以求出AA′的值.
点评:首先通过作辅助线把实际问题转换到直角三角形中,然后在图形中找到三角板的宽与角度的关系是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
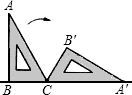 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C接顺时针方向旋转到A′B′C′的位置.若BC=15cm,那么顶点A从开始到结束所经过的路径长为( )
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C接顺时针方向旋转到A′B′C′的位置.若BC=15cm,那么顶点A从开始到结束所经过的路径长为( )| A、10πcm | B、30πcm | C、15πcm | D、20πcm |
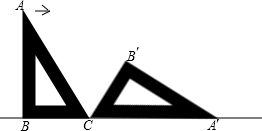 如图,一块含有30°角的直角三角形ABC,在水平桌面上绕点C按顺时针方向旋转到 A′B′C′的位置.若BC的长为15cm,那么顶点A从开始到结束所经过的路径长为
如图,一块含有30°角的直角三角形ABC,在水平桌面上绕点C按顺时针方向旋转到 A′B′C′的位置.若BC的长为15cm,那么顶点A从开始到结束所经过的路径长为 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC的长为15cm,那么顶点A从开始到结束所经过的路径长为多少?
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC的长为15cm,那么顶点A从开始到结束所经过的路径长为多少? 如图,一块含有30°角(∠BAC=30°)的直角三角板ABC,绕着它的一个锐角顶点A旋转后它的直角顶点落到原斜边上,那么旋转角是
如图,一块含有30°角(∠BAC=30°)的直角三角板ABC,绕着它的一个锐角顶点A旋转后它的直角顶点落到原斜边上,那么旋转角是 如图,一块含有30°角(∠BAC=30°)的直角三角板ABC,在水平的桌面上绕A点按顺时针方向旋转到AB′C′的位置,点B、A、C′在一直线上,那么旋转角是
如图,一块含有30°角(∠BAC=30°)的直角三角板ABC,在水平的桌面上绕A点按顺时针方向旋转到AB′C′的位置,点B、A、C′在一直线上,那么旋转角是