题目内容
 如图,一块含有30°角(∠BAC=30°)的直角三角板ABC,在水平的桌面上绕A点按顺时针方向旋转到AB′C′的位置,点B、A、C′在一直线上,那么旋转角是
如图,一块含有30°角(∠BAC=30°)的直角三角板ABC,在水平的桌面上绕A点按顺时针方向旋转到AB′C′的位置,点B、A、C′在一直线上,那么旋转角是150
150
度.分析:由旋转的性质可得:∠CAC′是旋转角,又由∠BAC=30°,点B、A、C′在一直线上,根据邻补角的定义,即可求得答案.
解答:解:根据旋转的性质可得:∠CAC′是旋转角,
∵∠BAC=30°,点B、A、C′在一直线上,
∴∠CAC′=180°-∠BAC=180°-30°=150°,
即旋转角是150°.
故答案为:150.
∵∠BAC=30°,点B、A、C′在一直线上,
∴∠CAC′=180°-∠BAC=180°-30°=150°,
即旋转角是150°.
故答案为:150.
点评:此题考查了旋转的性质与旋转角的定义.此题比较简单,注意掌握旋转角是解此题的关键,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
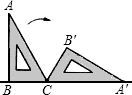 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C接顺时针方向旋转到A′B′C′的位置.若BC=15cm,那么顶点A从开始到结束所经过的路径长为( )
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C接顺时针方向旋转到A′B′C′的位置.若BC=15cm,那么顶点A从开始到结束所经过的路径长为( )| A、10πcm | B、30πcm | C、15πcm | D、20πcm |
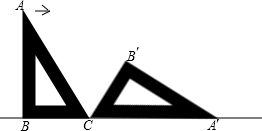 如图,一块含有30°角的直角三角形ABC,在水平桌面上绕点C按顺时针方向旋转到 A′B′C′的位置.若BC的长为15cm,那么顶点A从开始到结束所经过的路径长为
如图,一块含有30°角的直角三角形ABC,在水平桌面上绕点C按顺时针方向旋转到 A′B′C′的位置.若BC的长为15cm,那么顶点A从开始到结束所经过的路径长为 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC的长为15cm,那么顶点A从开始到结束所经过的路径长为多少?
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置.若BC的长为15cm,那么顶点A从开始到结束所经过的路径长为多少? 如图,一块含有30°角(∠BAC=30°)的直角三角板ABC,绕着它的一个锐角顶点A旋转后它的直角顶点落到原斜边上,那么旋转角是
如图,一块含有30°角(∠BAC=30°)的直角三角板ABC,绕着它的一个锐角顶点A旋转后它的直角顶点落到原斜边上,那么旋转角是