题目内容
?ABCD中，AB=3，BC=5，则?ABCD的周长等于________．
16
分析：由于平行四边形的对边相等，所以AB=CD，BC=DA，所以周长可求解．
解答：∵四边形ABCD是平行四边形
∴AB=CD，AD=BC
∴?ABCD的周长：2（AB+BC）=16．
故答案为16．
点评：平行四边形的性质有：（1）平行四边形的对边平行且相等．（2）平行四边形的对角相等；（3）平行四边形的对角线互相平分．
分析：由于平行四边形的对边相等，所以AB=CD，BC=DA，所以周长可求解．
解答：∵四边形ABCD是平行四边形
∴AB=CD，AD=BC
∴?ABCD的周长：2（AB+BC）=16．
故答案为16．
点评：平行四边形的性质有：（1）平行四边形的对边平行且相等．（2）平行四边形的对角相等；（3）平行四边形的对角线互相平分．
练习册系列答案
相关题目
7、如图，平行四边形ABCD中，AB=3，BC=5，AC的垂直平分线交AD于E，若AC=4则．①△CDE的周长比△CDA的周长小4，②∠ACD=90°；③AE=ED=CE；④四边形ABCD面积是12．则上述结论正确的是（ ）
14、如图，在矩形ABCD中，AB=6cm，将矩形ABCD折叠，使点B与点D重合，点C落在C′处，若AE：BE=1：2，则折痕EF的长为如图，在?ABCD中，AB：AD=3：2，∠ADB=60°，那么cosA的值等于（ ）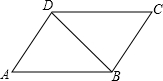
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
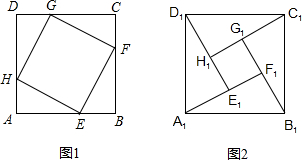
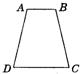5、如图，在等腰梯形ABCD中，AB∥DC，AB=998，DC=1001，AD=1999，点P在线段AD上，则满足条件∠BPC=90°的点P的个数为（ ）