Question

随着绿城南宁近几年城市建设的快速发展，对花木的需求量逐年提高．某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润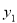与投资量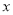成正比例关系，如图（1）所示；种植花卉的利润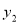与投资量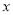成二次函数关系，如图（2）所示（注：利润与投资量的单位：万元）

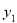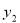（1）分别求出利润与关于投资量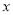的函数关系式；

（2）如果这位专业户以8万元资金投入种植花卉和树木，他至少获得多少利润？他能获取的最大利润是多少？

Answer 1

（1）y1=2x（x≥0）；y=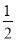x2（x≥0）；（2）当x=8时，z的最大值是32．

【解析】

试题分析：（1）可根据图象利用待定系数法求解函数解析式；

（2）根据总利润=树木利润+花卉利润，列出函数关系式，再求函数的最值．

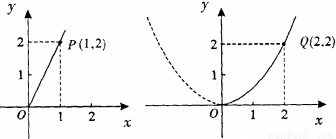
试题解析：（1）设y1=kx，由图①所示，函数y1=kx的图象过（1，2），

所以2=k•1，k=2，

故利润y1关于投资量x的函数关系式是y1=2x（x≥0）；

∵该抛物线的顶点是原点，

∴设y2=ax2，

由图②所示，函数y2=ax2的图象过（2，2），

∴2=a•22，a=，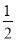

故利润y2关于投资量x的函数关系式是：y=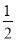x2（x≥0）；

（2）设这位专业户投入种植花卉x万元（0≤x≤8），则投入种植树木（8-x）万元，他获得的利润是z

元，根据题意，

得z=2（8-x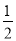）+x2=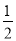x2-2x+16=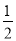（x-2）2+14，

当x=2时，z的最小值是14，

∵0≤x≤8，

∴-2≤x-2≤6，

∴（x-2）2≤36，

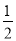∴（x-2）2≤18，

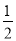∴（x-2）2+14≤18+14=32，

即z≤32，此时x=8，

答：当x=8时，z的最大值是32．

考点：1．二次函数的应用；2．一次函数的应用．