题目内容
计算化简求值:
(1)
+
(
+
);
(2)先化简,再求值:
÷(x-
),其中x=
+1.
(1)
| 1 | ||
|
| 3 |
| 3 |
| 6 |
(2)先化简,再求值:
| x+1 |
| x |
| 1+x2 |
| 2x |
| 2 |
分析:(1)先把
分母有理化和二次根式的乘法运算得到原式=
+(
)2+
•
,化简得到
+1+3+3
,然后合并同类二次根式即可;
(2)先把括号内通分得到原式=
÷
=
÷
,再把分子因式分解和除法转化为乘法得
•
,然后进行约分,接着把x的值代入计算即可.
| 1 | ||
|
| ||||
(
|
| 3 |
| 3 |
| 6 |
| 2 |
| 2 |
(2)先把括号内通分得到原式=
| x+1 |
| x |
| 2x2-(1+x2) |
| 2x |
| x+1 |
| x |
| x2-1 |
| 2x |
| x+1 |
| x |
| 2x |
| (x+1)(x-1) |
解答:解:(1)原式=
+(
)2+
•
=
+1+3+3
=4
+4;
(2)原式=
÷
=
÷
=
•
=
,
当x=
+1时,原式=
=
.
| ||||
(
|
| 3 |
| 3 |
| 6 |
=
| 2 |
| 2 |
=4
| 2 |
(2)原式=
| x+1 |
| x |
| 2x2-(1+x2) |
| 2x |
=
| x+1 |
| x |
| x2-1 |
| 2x |
=
| x+1 |
| x |
| 2x |
| (x+1)(x-1) |
=
| 2 |
| x-1 |
当x=
| 2 |
| 2 | ||
|
| 2 |
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后进行二次根式的加减运算.也考查了分式的化简求值.

练习册系列答案
相关题目
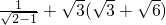 ;
; ,其中
,其中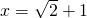 .
. ;
; ,其中
,其中 .
.