Question

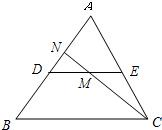
如图，DE是△ABC的中位线，M是DE的中点，CM的延长线交AB于点N，则S_△DMN：S_{四边形ANME}等于（　　）

A．1：5

B．1：4

C．2：5

D．2：7

Answer 1

∵DE是△ABC的中位线，
∴DE∥BC，DE=

1

2

BC，
若设△ABC的面积是1，根据DE∥BC，得△ADE∽△ABC，
∴S_△ADE=

1

4

，
连接AM，根据题意，得S_△ADM=

1

2

S_△ADE=

1

8

S_△ABC=

1

8

，
∵DE∥BC，DM=

1

4

BC，
∴DN=

1

4

BN，
∴DN=

1

3

BD=

1

3

AD．
∴S_△DNM=

1

3

S_△ADM=

1

24

，
∴S_{四边形ANME}=

1

4

-

1

24

=

5

24

，
∴S_△DMN：S_{四边形ANME}=

1

24

：

5

24

=1：5．
故选A．