题目内容
17. 如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.8m,则排水管内水的深度为0.8m.
如图,水平放置的圆柱形排水管道的截面直径是1m,其中水面的宽AB为0.8m,则排水管内水的深度为0.8m.
分析 过O点作OC⊥AB,C为垂足,交⊙O于D,连OA,根据垂径定理得到AC=BC=0.5m,再在Rt△AOC中,利用勾股定理可求出OC,即可得到CD的值,即水的深度.
解答 解:如图,过O点作OC⊥AB,C为垂足,交⊙O于D、E,连OA,
OA=0.5m,AB=0.8m,
∵OC⊥AB,
∴AC=BC=0.4m,
在Rt△AOC中,OA2=AC2+OC2,
∴OC=0.3m,
则CE=0.3+0.5=0.8m,
故答案为:0.8.
点评 本题考查了垂径定理的应用,掌握垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧是解题的关键,注意勾股定理的运用.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
7.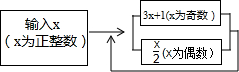 在数学活动课上,同学们利用如图的程序进行计算,发现无论x取任何正整数,结果都会进入循环,下面选项一定不是该循环的是( )
在数学活动课上,同学们利用如图的程序进行计算,发现无论x取任何正整数,结果都会进入循环,下面选项一定不是该循环的是( )
 在数学活动课上,同学们利用如图的程序进行计算,发现无论x取任何正整数,结果都会进入循环,下面选项一定不是该循环的是( )
在数学活动课上,同学们利用如图的程序进行计算,发现无论x取任何正整数,结果都会进入循环,下面选项一定不是该循环的是( )| A. | 4,2,1 | B. | 2,1,4 | C. | 1,4,2 | D. | 2,4,1 |
8.反比例函数y=-$\frac{2}{x}$的图象上有两点P1(x1,y1),P2(x2,y2),若x1<0<x2,则下列结论正确的是( )
| A. | y1<y2<0 | B. | y1<0<y2 | C. | y1>y2>0 | D. | y1>0>y2 |
12.若$\frac{y}{x}$=$\frac{3}{4}$,则$\frac{x+y}{x}$的值为( )
| A. | 1 | B. | $\frac{4}{7}$ | C. | $\frac{5}{4}$ | D. | $\frac{7}{4}$ |
2.方程2x-1=3的解是( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
17.-7的倒数( )
| A. | -$\frac{1}{7}$ | B. | 7 | C. | -7 | D. | $\frac{1}{7}$ |
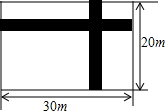 如图所示,在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地,若耕地面积需要551平方米,设修建的路宽为x米,根据题意,可列方程为(30-x)(20-x)=551.
如图所示,在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地,若耕地面积需要551平方米,设修建的路宽为x米,根据题意,可列方程为(30-x)(20-x)=551.