Question

【题目】如图，矩形中，，．点从向以每秒个单位的速度运动，以为一边在的右下方作正方形．同时垂直于的直线也从向以每秒个单位的速度运动，当经过________秒时．直线和正方形开始有公共点？

Answer 1

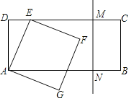
【答案】

【解析】

过F作FQ⊥DC于Q，证明△ADE≌△EQF，根据全等三角形的性质可得AD=EQ=4，当直线MN和正方形AEFG开始有公共点时DQ+CM≥10，由此即可解答．

过F作FQ⊥DC于Q，

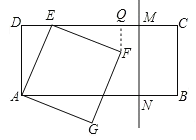
∵四边形AEFG是正方形，

∴∠AEF=90°，AE=EF，

∴∠DEA+∠FEQ=90°，

∵四边形ABCD是矩形，

∴∠D=90°，

∴∠DAE+∠DEA=90°，

∴∠FEQ=∠DAE，

在△ADE和△EQF中，

∵∠D=∠EQF=90°，∠DAE=∠FEQ，AE=EF，

∴△ADE≌△EQF，

∴AD=EQ=4，

当直线MN和正方形AEFG开始有公共点时，DQ+CM≥10，

∴2t+4+3t≥10，

解得t≥，

∴当经过秒时．直线MN和正方形AEFG开始有公共点.

故答案为：．