��Ŀ����
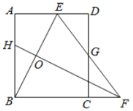
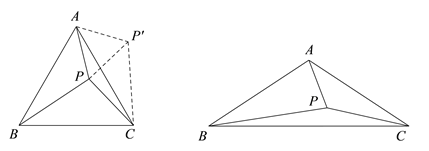
����Ŀ������ABC�У�AB=AC����BAC=������P�ǡ�ABC��һ�㣬��![]() ������PB����̽��PA��PB��PC����ĵ�����ϵ��
������PB����̽��PA��PB��PC����ĵ�����ϵ��
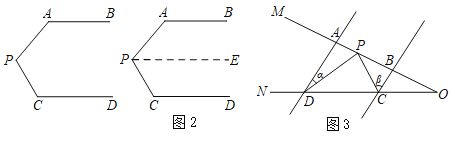
ͼ1 ͼ2
��1������=60��ʱ������ABP�Ƶ�A��ʱ����ת60��õ�![]() ������
������![]() ����ͼ1��ʾ��
����ͼ1��ʾ��
��![]() ��
��![]() ����֤��
����֤��![]() �ǵȱ������Σ�����
�ǵȱ������Σ�����![]() �ɵ���APC�Ĵ�СΪ �ȣ������õ�
�ɵ���APC�Ĵ�СΪ �ȣ������õ�![]() ��ֱ�������Σ��������Եõ�PA��PB��PC����ĵ�����ϵΪ ��
��ֱ�������Σ��������Եõ�PA��PB��PC����ĵ�����ϵΪ ��
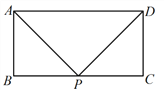
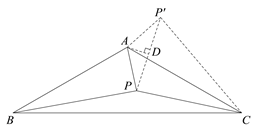
��2����ͼ2������=120��ʱ����ο���1���еķ�����̽��PA��PB��PC����ĵ�����ϵ��������֤����
��3��PA��PB��PC����ĵ�����ϵΪ ��
���𰸡���1��150�� ![]() ��2��֤����������3��
��2��֤����������3��![]()
�������������������1��������ת�任�����ʵõ���PAP��Ϊ�ȱ������Σ��õ���P��PC��90�������ݹ��ɶ�����ɣ�
��2����ͼ2��������ABP�Ƶ�A��ʱ����ת120���õ���ACP��������PP������AD��PP����D���������ҵĶ���õ�PP����![]() PA�����ݹ��ɶ�����ɣ�
PA�����ݹ��ɶ�����ɣ�
��3���루2�����ƣ�������ת�任�����ʡ����ɶ��������ҡ����ҵĹ�ϵ���㼴�ɣ�
���������
�⣺��1���ߡ�ABP�ա�ACP����
��AP��AP����
����ת�任�����ʿ�֪����PAP����60����P��C��PB��
���PAP��Ϊ�ȱ������Σ�
���APP����60����
�ߡ�PAC����PCA��![]() ��60�� ��30����
��60�� ��30����
���APC��150����
���P��PC��90����
��PP��2��PC2��P��C2��
��PA2��PC2��PB2��
�ʴ�Ϊ��150��PA2��PC2��PB2��
��2����ͼ����![]() ����ʹ
����ʹ![]() ������
������![]() ��
�� ![]() ������A��AD��
������A��AD��![]() ��D�㣮
��D�㣮
��![]() ����
����
��![]() ��
��
��![]() ��
��
��AB��AC�� ![]() ��
��
��![]() .
.
��![]() ��
�� ![]() ����
����
��AD��![]() ��
��
��![]() ��.
��.
����Rt ![]() ��
�У� ![]() .
.
��![]() ��
��
��![]() ����
����
��![]() ��.
��.
��![]() ����
����
����Rt ![]() ��
�У� ![]() .
.
��![]() ��
��
��3����ͼ2���루2���ķ������ƣ�
������ABP�Ƶ�A��ʱ����ת���õ���ACP��������PP����
��AD��PP����D��
����ת�任�����ʿ�֪����PAP��������P��C��PB��
���APP����90����![]() ��
��
�ߡ�PAC����PCA��![]() ��
��
���APC��180����![]() ��
��
���P��PC����180����![]() ������90����
������90����![]() ����90����
����90����
��PP��2��PC2��P��C2��
�ߡ�APP����90����![]() ��
��
��PD��PAcos��90����![]() ����PAsin
����PAsin![]() ��
��
��PP����2PAsin![]() ��
��
��4PA2sin2![]()
�ʴ�Ϊ��4PA2sin2![]() ��PC2��PB2��
��PC2��PB2��