��Ŀ����
����Ŀ�����壺��һ���ڱ���ȣ��������ǵļн���ֱ�ǵ��ı��ν�������ֱ���ı��Σ�
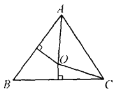
(1)��ͼ 1������ֱ���ı��� ABCD��AB��BC����ABC��90��.
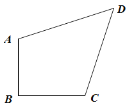
ͼ 1
���� AB��CD��1��AB��CD����Խ��� BD �ij���
���� AC��BD����֤��AD��CD��
(2) ��ͼ 2������ ABCD �ij���Ϊ���� ![]() ��14x+40=0 �����������У�BC >AB������ E �� A ��������� 1 ����λÿ����ٶ����յ� D �˶���ͬʱ�� F �� C ��������� 2 ����λÿ����ٶ����յ� B �˶������� E��F �˶�������ʹ�ı��� ABFE �ǵ���ֱ���ı���ʱ���� EF �ij���
��14x+40=0 �����������У�BC >AB������ E �� A ��������� 1 ����λÿ����ٶ����յ� D �˶���ͬʱ�� F �� C ��������� 2 ����λÿ����ٶ����յ� B �˶������� E��F �˶�������ʹ�ı��� ABFE �ǵ���ֱ���ı���ʱ���� EF �ij���

ͼ 2
���𰸡���1����BD=![]() ����֤������⣻��2��
����֤������⣻��2��![]() ��
��![]()
��������
��1����ֻҪ֤���ı���ABCD�������μ��ɽ�����⣻
��ֻҪ֤����ABD�ա�CBD�����ɽ�����⣻
��2���Ƚⷽ�̣����AB��BC�ij��ȣ�Ȼ��������⣬���۵�AB=AE����AB=BFʱ���ı���ABFE�ǵ���ֱ���ı���.��AB=AE=4ʱ������EF����F��FG��AE����AE�ڵ�G���ɵ��˶���ʱ��Ϊ4s���ɵ�CF=8��Ȼ��õ�GE=2�����ù��ɶ����õ�EF�ij��ȣ���AB=BF=4ʱ������EF������E��EH��BF����BF�ڵ�H ���ɵ�CF=6���˶���ʱ��Ϊ3s���ɵ�AE=3��Ȼ��õ�FH=1�����ù��ɶ������EF�ij���.
�⣺��1���١�AB=CD=1��AB��CD��
���ı���ABCD��ƽ���ı��Σ�
��AB=BC��
���ı���ABCD�����Σ�
�ߡ�ABC=90����
���ı���ABCD�������Σ�
��BD=AC=![]() ��
��
����ͼ1�У�����AC��BD��
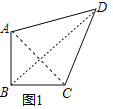
��AB=BC��AC��BD��
���BAC=��BCA��
���ABD=��CBD��
��BD=BD��
���ABD�ա�CBD��
��AD=CD��
��2����AB��BC�ij����Ƿ���![]() ��14x+40=0����������
��14x+40=0����������
�ⷽ�̣�![]() ��14x+40=0�ã�
��14x+40=0�ã�![]() ��
��
��BC >AB��
��AB=4��BC=10.
�������⣬��AB=AE��AB=BFʱ���ı���ABFE�ǵ���ֱ���ı��Σ�
��AB=AEʱ����ͼ������EF����F��FG��AE����AE�ڵ�G��
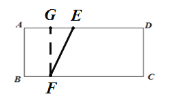
��AB=AE=4���ı���ABFG�Ǿ��Σ�
���˶���ʱ��Ϊ��![]() ��
��
��CF=![]() ��
��
��BF=2=AG��
��GE=2��GF=AB=4��
�ɹ��ɶ����ã�EF=![]() ��
��
��AB=BFʱ����ͼ������EF������E��EH��BF����BF�ڵ�H��
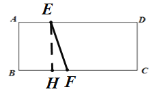
��AB=BF=4��
��CF=10-4=6��
���˶���ʱ��Ϊ��![]() ��
��
��AE=3��EH=AB=4
��FH=4-3=1��
�ɹ��ɶ����ã�EF=![]() ��
��
��EF�ij�����![]() ��
��![]() .
.